Игнаси Белда - Том 33. Разум, машины и математика. Искусственный интеллект и его задачи

Нейронная сеть формулирует прогнозы, однако неизвестно, как именно она при этом рассуждает. Некоторые сравнивают нейронные сети с магическим кристаллом.

С конца 90-х годов многие специалисты по теории вычислений интенсивно работают над созданием новых вычислительных методов, которые позволят устранить эти недостатки или хотя бы снизить их негативный эффект. Окончательное решение в начале XXI века предложила группа под руководством Владимира Вапника из знаменитой компании AT&T Bell Labs, специализирующейся на телекоммуникациях и производстве электроники. Вапник разработал метод опорных векторов (англ. SVM — Support Vector Machine ), при котором для решения линейно неразделимых задач вводятся новые, искусственные измерения, позволяющие преобразовать исходную задачу в линейно разделимую.

Метод опорных векторов лишен большинства недостатков нейронных сетей, поэтому сегодня он пришел им на смену практически во всех областях компьютерных технологий. Тем не менее нейронные сети до сих пор используются в промышленности, в частности в робототехнике, благодаря простой аппаратной реализации.

Как вы уже знаете, машинное обучение может применяться во всех областях науки и техники. Но можно ли пойти дальше и применить его в образовании? Как преподаватель определяет уровень знаний учеников? Можно ли автоматизировать некоторые субъективные критерии, которые используют школьные учителя и университетские преподаватели для оценки знаний учащихся? Можно ли спрогнозировать уровень знаний ученика, не проводя экзаменов? На все эти вопросы поможет ответить дерево принятия решений.

Исчезнет ли подобная картина в будущем? Этого наверняка хотят многие студенты.

Деревья принятия решений крайне просты, но очень эффективны для распознавания образов. Они позволяют выяснить, какие переменные играют определяющее значение при отнесении выборки к тому или иному классу. Рассмотрим пример. Допустим, что мы хотим спрогнозировать оценки студентов и располагаем следующими исходными данными.

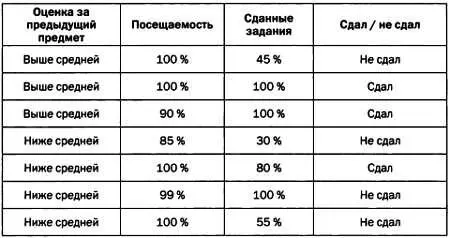
Хорошее дерево принятия решений, составленное с учетом этих данных, может выглядеть следующим образом.

* * *

ИНФОРМАЦИОННОЕ ДЕРЕВО

Дерево — это структура данных, которая очень широко используется в инженерном деле, так как позволяет строить иерархии данных. При работе с деревьями используются особые понятия.

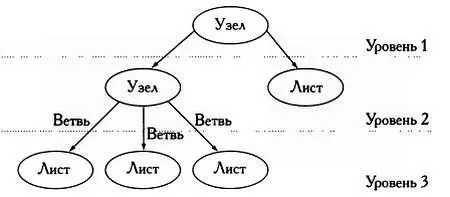
Данные, представленные в дереве, называются узлами. Эти узлы, представляющие единицы информации, делятся на разные уровни и связываются между собой ветвями. Узел, связанный с узлом более высокого уровня, называется потомком, узел, связанный с узлом низшего уровня, — родителем. Узлы, не имеющие потомков, называются листьями.

* * *

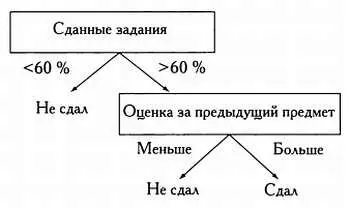
В этом случае посещаемость не является определяющей переменной, поэтому не представлена в виде узла дерева. Существуют различные методологии, позволяющие определить, является ли переменная модели дискриминантной (иными словами, можно ли разделить выборку на группы в зависимости от значений этой переменной). В основе одной из самых популярных методологий лежит понятие энтропии Шеннона. В рамках этой методологии для каждого уровня дерева определяется переменная, порождающая меньше всего энтропии. Именно эта переменная и будет дискриминантной для рассматриваемого уровня. Рассмотрим метод подробнее.

Энтропия Шеннона Sрассчитывается по следующей формуле:

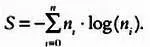
Попробуем применить это понятие в нашей задаче об экзаменах. На первом уровне дерева необходимо проанализировать энтропию, порождаемую каждой переменной. Первая переменная — «оценка за предыдущий предмет». Если мы разделим выборки в зависимости от значений этой переменной, получим два подмножества выборок. Для первого подмножества энтропия Шеннона будет равна

S Оценка за предыдущий предмет ниже средней = -0,75∙ log(0,75)— 0,25∙ log(0,25)= 0,56,

так как среди студентов, которые в прошлом году получили оценку ниже средней, не сдали экзамен 75 %, сдали — 25 %. Для второго множества энтропия Шеннона будет равна

S Оценка за предыдущий предмет ниже средней = -0,33∙ log(0,33)— 0,67∙ log(0,67)= 0,64,

так как треть студентов, которые в прошлом году получили оценку выше средней, не сдали экзамен, две трети студентов — сдали.

Подобные расчеты повторяются для каждой переменной. Следующая переменная — «посещаемость». Для простоты установим граничное значение посещаемости, равное 95 %. В этом случае

S Посещаемость выше 95 %= -0,6∙ log (0,6)— 0,4∙ log(0,4)= 0,67;

S Посещаемость выше 95 %= -0,5∙ log (0,5)— 0,5∙ log(0,5)= 0,69

Наконец, рассмотрим переменную «сданные задания» и вновь для простоты разобъем выборку на 2 группы, выделив тех, кто сдал больше и меньше 60 % заданий.

Имеем:

S Сдано более 60 % заданий= -0,75∙ log(0,75)— 0,25∙ log(0,25)= 0,56;

и

S Сдано более 60 % заданий= -1∙ log(1)= 0

Следовательно, наилучшей дискриминантной переменной будет последняя, так как энтропия подмножеств, выделенных на ее основе, равна 0,56 и 0.

В этом случае все представители обучающей выборки, сдавшие менее 60 % заданий, не сдали экзамен, следовательно, эту ветвь дерева можно не рассматривать.

Но другая ветвь содержит одинаковое число студентов, сдавших и не сдавших экзамен. Следовательно, необходимо продолжить анализ, не учитывая уже дискриминированные выборки.

Теперь остались только две переменные, которые могут повлиять на итоговое решение: «оценка за предыдущий предмет» и «посещаемость». Значения энтропии Шеннона для групп, выделенных в зависимости от значений первой дискриминантной переменной, таковы:

S Оценка за предыдущий предмет ниже средней= -0,5∙ log (0,5)— 0,5∙ log (0,5)= 0,69;