Игнаси Белда - Том 33. Разум, машины и математика. Искусственный интеллект и его задачи

Метки упрощают избирательное взаимодействие между агентами, так как позволяют различать экземпляры одного и того же класса агентов или различные составные части агента. На основе меток возможна реализация фильтров, схем сотрудничества, а также видообразование. Агенты также могут сохранять агрегированное состояние, и их метки будут оставаться неизменными, даже если будут меняться составные части агента более высокого уровня. По сути, нанесение меток — механизм, упрощающий организацию агентов и коммуникацию между ними.

Второе свойство: нелинейность

Свойство линейности лежит в основе множества математических дисциплин, начиная от арифметики и заканчивая алгебраической топологией, не говоря уже о дифференциальном исчислении. Функция линейна, если ее значение представляет собой всего лишь взвешенную сумму ее аргументов (независимо от их значений). К примеру, функция 4х + 2у — z линейна, функция 4 sinx — 2y -z — нет.

Использование линейных методов в математике и инженерном деле настолько важно, что сегодня большая часть профессиональной деятельности любого инженера и ученого заключается в поиске линейных функций, максимально точно описывающих те или иные явления природы. К сожалению, ни один из этих методов неприменим для изучения сложных адаптивных систем. По сути, одна из важнейших особенностей таких систем заключается в том, что их совокупное поведение намного сложнее суммы поведений отдельных частей, из чего, по определению, следует нелинейность.

Прекрасный пример, иллюстрирующий нелинейности в природе и сложных адаптивных системах, — взаимодействие «производитель — потребитель» и его частный случай — взаимодействие «хищник — жертва». Представьте себе лес, где живет D хищников (например, лис) и Ржертв (например, зайцев). Если вероятность того, что лиса поймает зайца, равна с, то ежедневно в лапы лис попадает с∙ Р∙ D зайцев. К примеру, если с= 0,5, D= 3 и Р= 10, то лисы поймают с ∙ Р∙ D= 0,5∙3∙10 = 15 зайцев. Если число лис и зайцев увеличится вчетверо, число пойманных зайцев возрастет еще больше: с∙ Р∙ D= 0,5∙12∙40 = 240. Как видите, этот результат нельзя получить простым сложением числа хищников и жертв.

Даже в сравнительно простой ситуации нелинейность может серьезно повлиять на агрегированную систему. Поэтому всегда говорят, что совокупное поведение сложной адаптивной системы сложнее, чем поведение ее составных частей.

* * *

МОДЕЛЬ ЛОТКИ — ВОЛЬТЕРРЫ

Уравнения, описывающие пример с лисами и зайцами, могут значительно усложняться. Исследователь Альфред Джеймс Лотка описал, как изменятся эти уравнения, если мы будем учитывать колебания численности хищников и жертв с течением времени. Допустим, что D(t)и P(t) — численность хищников и жертв в момент времени t. В каждый момент времени рождается n и умирает m хищников. Следовательно, формула, описывающая изменение численности хищников с течением времени, записывается так: D(t + 1)= D (t)+ nD(t)— mD(t). Аналогично изменение численности жертв описывается уравнением: Р(t + 1)= Р(t)+ n'Р(t)— mV(t). Следует учесть, что рост числа жертв означает рост рождаемости хищников, что можно выразить, к примеру, с помощью постоянной r.

Число взаимодействий «жертва — хищник», как мы показали, равно cPD. Следовательно, новое уравнение, описывающее численность хищников, будет выглядеть так:

D(t+1)= D(t)+ nD(t)— mD(t)+ r[cP(t)∙ D(t)]

Изменение численности жертв будет происходит прямо противоположным образом: при любом взаимодействии «хищник — жертва» численность жертв будет сокращаться. Уравнение численности жертв будет иметь вид:

P(t+1)= P(t)+ r[P(t)— m'P(t)— r[cP(t)∙ D(t)].

Если теперь мы зафиксируем значения постоянных и будем решать эти уравнения для последовательных моментов времени, то увидим, что D(t) и P(t)будут колебаться, а хищники и жертвы будут последовательно переживать циклы изобилия и голода.

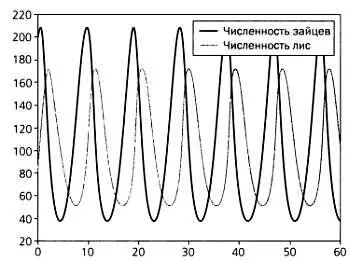
График, описывающий колебания численности зайцев и лис с течением времени согласно модели Лотки — Вольтерры.

Третье свойство: формирование потоков

Потоки возникают на всех уровнях сложных адаптивных систем, где присутствуют узлы, носители и переносимые ресурсы. Ограничимся двумя примерами сложных адаптивных систем. Первый — центральная нервная система живого организма, где узлами являются нейроны, носителями — соединяющие их синапсы, а переносимым ресурсом — электрические импульсы. Второй пример — потоки в экосистеме, где узлами являются виды, носителем — пищевая цепь, а переносимым ресурсом — энергия, представленная в виде биохимических элементов (потребляемого белка, сахара и так далее).

В общем случае узлы являются средствами обработки ресурса, а связи определяют взаимодействия между узлами. Следует учесть, что в сложной адаптивной системе сеть взаимодействий может меняться, а узлы и связи могут возникать и исчезать.

Эти особенности и обеспечивают адаптируемость системы к среде и позволяют ей корректировать свое поведение в зависимости от текущей ситуации.

Нанесение меток — один из самых важных механизмов сложных адаптивных систем для определения потоков: метки могут определять, какие связи играют важнейшую роль при переносе ресурсов.

Потоки обладают двумя свойствами, представляющими интерес при изучении работы сложных адаптивных систем. Первое свойство заключается в том, что потоки вносят в систему эффект мультипликатора. К примеру, в такой сложной адаптивной системе, как экономика страны, перенос денег от одного узла к другому (например, между банками) исполняет роль денежного мультипликатора. Второе интересное свойство — способность создания циклов с целью переработки. Обратите внимание, как на схеме нелинейно возрастает объем промышленного производства в сложной адаптивной системе — производственной цепочке изготовления автомобилей — при переработке и в ее отсутствие.

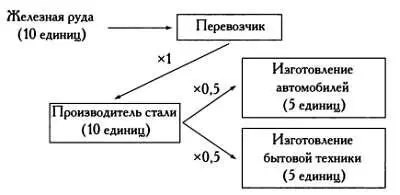
В первом сценарии производитель стали преобразует железную руду в сталь с эффективностью 100 % (то есть с коэффициентом 1). Далее 50 %, то есть половина произведенной стали, используется для производства автомобилей, оставшиеся 50 % — для изготовления бытовой техники. Если мы для простоты предположим, что из каждой единицы стали изготавливается автомобиль или единица бытовой техники, то получим, что в конце потока будет произведено 5 автомобилей и 5 единиц бытовой техники.