Энрике Грасиан - Мир математики. т.3. Простые числа. Долгая дорога к бесконечности

Нужно отметить, что малая теорема Ферма содержит необходимое, но не достаточное условие: если р — простое число, то условие выполняется, но выполнение условия не означает, что р будет простым. Например, если взять р = 4 и а = 5, то 5 4— 5 = 620 делится на 4, но 4 = 2 х 2 является составным числом.

Числа Ферма

«Числами Ферма» называются натуральные числа вида:

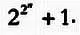
Они обозначаются буквой F (по имени Ферма) с соответствующим индексом (n), так что F 0 обозначает первое число Ферма, F 1 — второе и так далее. Посчитаем значения первых пяти чисел Ферма, учитывая, что любое число в степени 0 равно 1:

2 0 = 1; 2 1= 2; 2 2= 4; 2 3= 8.

Подставляя в формулу, получим:

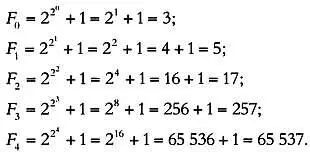
Ферма предположил, что все числа, полученные таким способом, являются простыми. Первые пять чисел — 3, 5, 17, 257 и 65537 — действительно простые.

Но при n = 5 получается число:

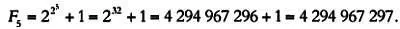
Ферма не смог определить, является ли это число простым. Но Эйлеру в 1732 г. удалось представить это число в виде произведения двух множителей:

4294967297 = 641 х 6700417.

Тем самым Эйлер показал, что гипотезы Ферма могут быть ложными. Нечто подобное произошло впервые. И хотя гипотеза оказалась ошибочной, числа Ферма продолжают играть важную роль — не только потому, что благодаря им возникли новые идеи и гипотезы, но и потому, что они оказались полезными для выявления простых чисел.

В настоящее время известно, что только первые пять чисел Ферма являются простыми. Но это вовсе не означает, что других простых чисел Ферма не существует: на самом деле их может быть бесконечное множество. Разложение на множители было проделано лишь для чисел Ферма с индексом до n = 11. Представление числа в виде произведения простых множителей является нелегкой задачей. Как мы позже покажем, эта трудность лежит в основе одного из самых популярных методов шифрования, используемых сегодня.

Не существует ни одной области классической математики, будь то дифференциальное и интегральное исчисление, дифференциальные уравнения, аналитическая и дифференциальная геометрия, теория чисел или теория рядов, в которой бы не появлялось имя швейцарского математика и физика Леонарда Эйлера(1707–1783) . Он был одним из самых плодовитых математиков своего времени. После его смерти в Санкт-Петербурге его сочинения продолжают вызывать восхищение и регулярно переиздаются Санкт-Петербургской Академией наук. Швейцарская академия наук планирует опубликовать полное собрание его работ, которое составит около 90 томов.

Банкнота 10 швейцарских франков 1997 г. выпуска с портретом Эйлераи изображениями гидравлической турбины, солнечной системы и света, проходящего через линзу. Все это иллюстрирует вклад Эйлера в математику.

Эйлер всегда проявлял особый интерес к простым числам. Он составил таблицу всех простых чисел от 1 до 100 000 и нашел формулы, которые позволяли ему получать невероятные количества таких чисел. Одной из наиболее интересных является следующая формула:

х 2+ х+ q,

которая генерирует простые числа для любых значений х , больших 0 и меньших q — 2.

Эйлер нашел все такие простые числа для q = 2, 3, 5, 7, 11 и 17. В то время математика была экспериментальной, ее целью было получение практических результатов, поэтому строгие доказательства часто отсутствовали. Однако в отличие от Ферма Эйлер не скрывал своей работы. Если у него было доказательство, он публиковал его, а если факт приводился без доказательства, значит, оно не было найдено.

Работы Эйлера привели к важным изменениям в мире математики, вызвав медленный, но неумолимый сдвиг научной мысли. Среди многочисленных достижений Эйлера есть три, которые оказали решающее влияние на дальнейшие исследования в теории простых чисел: понятия функции, бесконечных сумм и мнимых величин.

Позже мы еще вернемся к ним.

Функции

Эйлер заложил основы того, что в последующие века будет называться математическим анализом. Именно он ввел обозначение функции, f(х) , которое используется и в настоящее время. Функция работает как устройство, которое преобразует числа в другие числа в соответствии с установленным правилом. (Мы имеем в виду действительные функции действительного переменного.) Например, если правило гласит, что к каждому числу нужно прибавить определенное число, например, 3, то функция записывается следующим образом:

f(х) = x + 3.

Теперь функцию можно применить к любым значениям переменной:

f(1)= 1 + 3 = 4;

f(2)= 2 + 3 = 5;

f(24)= 24 + 3 = 27;

f(0,32)= 0,32 + 3 = 3,32.

Действительные функции действительного переменного ставят в соответствие каждому действительному числу другое действительное число. Например, функция f(x )= 2х+ 1каждое значение х увеличивает в два раза и прибавляет единицу. Составим таблицу значений этой функции:

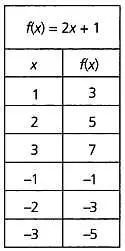
Эта таблица позволяет построить график функции по вышеуказанным координатам точек:

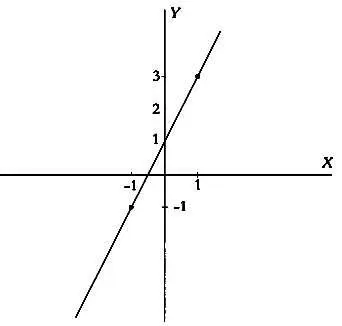
Это очень простой график, он представляет из себя прямую линию, построить которую можно всего по двум точкам. С другой стороны, функция вида f(х)= х 2будет иметь следующую таблицу значений:

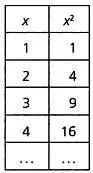
И график этой функции уже не так легко построить:

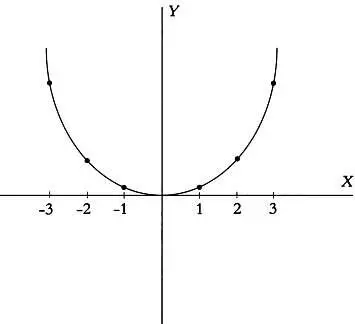
Фактически, чем больше у нас точек, тем более точный график можно построить, но если выражение функции не является линейным, то есть если переменная х возводится в степень, большую единицы, графиком функции является кривая линия.

В некоторых случаях эта кривая известна, а в других она оказывается очень непредсказуемой и ее нельзя построить вручную. Одним из величайших достижений Эйлера является представление сложных функций в простых терминах.