Энрике Грасиан - Мир математики. т.3. Простые числа. Долгая дорога к бесконечности

Бесконечные суммы

Еще Эйлер для обозначения суммы, или «суммирования», ввел специальный символ, который используется и в современной математике. Это знак Σ— заглавная буква «сигма» греческого алфавита, а также первая буква слова «сумма».

Выражение суммирования записывается следующим образом:

Σ i=5 j=1 i,

где есть переменная, в данном случае i , и индексы, показывающие, как эта переменная изменяется. В данном примере i изменяется от 1 до 5. Таким образом:

Σ i=5 j=1 i= 1 + 2 + 3 + 4 + 5;

Σ i=3 j=1 (n+ 1)= (1 + 1) + (2 + 1) + (3 + 1);

Σ i=4 j=1 n 2= 1 2+ 2 2+ 3 2+ 4 2.

Обычно запись выражения упрощают, указывая в качестве верхнего индекса лишь последнее значение переменной:

Σ 5 j=1 i= 1 + 2 + 3 + 4 + 5.

Это означает, что i меняется от 1 до 5.

Если верхний предел не является числом, то используется символ бесконечности, означающий, что сумма бесконечна. Например:

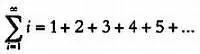
Хотя это может показаться странным, но существуют бесконечные суммы, результат которых является конечным числом. Ряды, имеющие такую сумму, называются сходящимися. Например, ряд

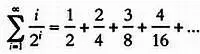
имеет конечную сумму, приблизительно равную 2. Так как члены ряда становятся все меньше и меньше, в какой-то момент каждый следующий член будет настолько мал, что его добавление ничего не изменит, и итоговая сумма будет конечным числом. Безусловно, это не совсем точное объяснение. Можно предположить, что ряд типа

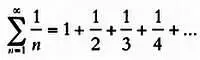
также имеет конечную сумму, но это не так. Данный ряд, которым особенно интересовался Эйлер, называется гармоническим. Эйлер использовал его, чтобы получить еще одно доказательство бесконечности множества простых чисел.

* * *

БАЗЕЛЬСКАЯ ЗАДАЧА

Братья Якоб (1654–1705) и Иоганн(1667–1748) Бернулли занимались изучением гармонических рядов. Особенно активно они работали в период между 1689 и 1704 гг. Именно они доказали, что некоторые ряды расходятся. Воодушевленные результатами, они взялись за ряд обратных квадратов:

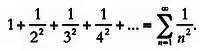
Якоб показал, что ряд сходится, и ему даже удалось доказать, что сумма ряда меньше или равна двум, но он не смог найти точное значение. Он так увлекся этой проблемой, что сказал: «Велика будет наша благодарность, если кто-нибудь найдет и сообщит нам о том, что до сих пор избегало нашего внимания». Эта проблема известна как «базельская задача», потому что Якоб заведовал кафедрой математики в университете швейцарского города Базеля, и именно там он произнес свои знаменитые слова.

Многие великие математики, в том числе Менголи и Лейбниц, не смогли решить эту задачу, не говоря уже о совместных усилиях братьев Бернулли. И лишь спустя 30 лет решение было найдено «волшебником» Эйлером. Результат был действительно впечатляющим:

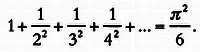
Эйлер писал об этом результате так:

«…Я сейчас обнаружил вопреки всем ожиданиям элегантное выражение для суммы ряда 1 + 1/4 + 1/9 + 1/16 + …, которое имеет отношение к квадратуре круга… Я обнаружил, что сумма этого ряда, умноженная на 6, равна квадрату длины окружности, диаметр которой — единица».

К сожалению, Якоб умер к тому времени, когда Эйлер опубликовал свои результаты. «Эх, если бы мой брат был жив!» — воскликнул Иоганн.

«Волшебником» Эйлера называли из-за совершенно магических методов, которые он использовал в доказательствах. На самом деле доказать этот результат совсем не сложно, но такой подход требует некоторых знаний высшей математики и показывает смелость Эйлера, который рассмотрел этот ряд в качестве полиномиальной функции, а затем связал его с разложением в ряд функции синуса. Отсюда и появилось число π, которое является одним из нулей синуса.

Иоганн Бернуллибыл учителем Эйлера и одним из лучших математиков своего времени.

* * *

Гармонический ряд расходится, и это означает, что сумма его членов бесконечна, но расходится он чрезвычайно медленно по сравнению с рядом вида

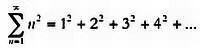
Работая с гармоническим рядом, Эйлер вывел функцию, вошедшую в историю как одна из важнейших функций математики: «дзета-функция Эйлера», которая в настоящее время несколько несправедливо называется «дзета-функцией Римана».

Для ее обозначения Эйлер использовал греческую букву ζ(дзета):

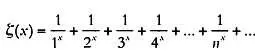
Если взять х = 1, то мы получим уже известный нам гармонический ряд 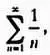причем мы знаем, что его сумма бесконечна. Однако Эйлер предполагал, что при х = 2 сумма ряда

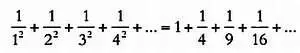
не будет бесконечной, так как здесь содержатся только некоторые члены гармонического ряда, а именно дроби с квадратами. Но найти сумму этого ряда было практически невозможно, используя знания того времени. Тем не менее Эйлеру удалось блестяще доказать следующее равенство:

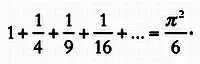
Эйлер сделал это открытие в возрасте 28 лет, хотя ему понадобилось еще шесть лет, чтобы отшлифовать доказательство. Неожиданное появление в выражении для суммы ряда числа π, которое встречается в формулах площади круга и длины окружности, вызвало удивление всего математического сообщества того времени. С помощью этого результата Эйлер смог решить одну из самых интригующих проблем того времени, так называемую «базельскую задачу».

Экспериментируя с дзета-функцией, Эйлер получил ряд результатов. Например, он уже знал, что при х , меньших или равных 1, сумма ряда бесконечна, и что, следовательно, ряд сходится только при х , больших 1.