Хавьер Фресан - Том. 22. Сон разума. Математическая логика и ее парадоксы

Образ машины может быть обманчивым, и читатель, возможно, поверит, что идеальная машина Тьюринга, о которой мы говорим, в состоянии вычислить значение любой функции, которую только можно себе представить. В действительности дело обстоит с точностью до наоборот: действия, скрытые между входным значением n и выходным значением f( n ), могут быть настолько сложными, что даже машина Тьюринга будет неспособна их выполнить. Чтобы читатель лучше понимал эту ситуацию, необходимо подробно объяснить, как работают машины, которые придумал Алан Тьюринг, когда ему было немногим больше двадцати лет.

Первым элементом машины Тьюринга является лента, не имеющая начала и конца (напомним, что речь идет об идеальной машине), разделенная на ячейки. В каждую ячейку помещается только один символ — 0 или 1. Эти символы соответствуют, как известно, двум возможным значениям истинности. Вторым элементом машины Тьюринга является устройство чтения-записи, способное определять, какой символ записан в определенной ячейке, и производить запись поверх него.

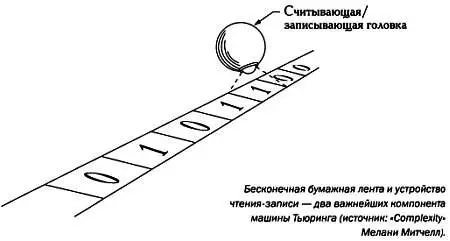
После прочтения любого символа устройство чтения-записи может повести себя пятью различными способами: стереть ранее записанное число и записать 0, заменить записанный символ на 1, сместиться вправо, сместиться влево (чтобы эти две операции могли быть выполнены, крайне важно, чтобы бумажная лента не имела ни начала, ни конца) или просто остановиться, никак не реагируя на прочитанный символ. Последовательность действий контролируется конечной последовательностью инструкций, которые указывают, как машина должна реагировать в каждом возможном случае. Например, первая инструкция может звучать так: «Если считан символ 1, сместиться влево и перейти к третьей инструкции». Все инструкции следуют одной и той же схеме.

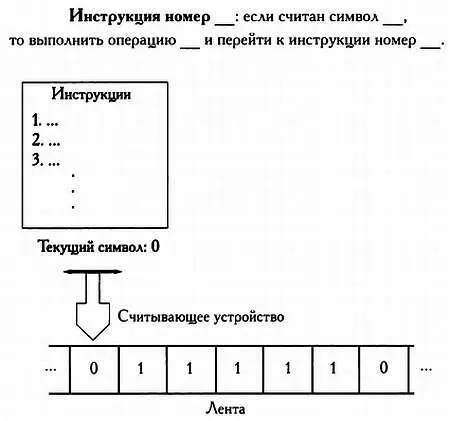
Принцип действия машины Тьюринга

(источник: «Complexity» Мелани Митчелл).

Как мы уже упоминали, инструкции нумеруются начиная с 1, используются символы 0 и 1, а допустимыми операциями являются запись 0 (0), запись 1(1), переход на ячейку вправо ( R ), переход на ячейку влево ( L ) или останов ( N ). Таким образом, любую инструкцию можно описать всего четырьмя параметрами. Если первая инструкция звучит так: «Если считан символ 1, сместиться влево и перейти к третьей инструкции», достаточно записать (#1, 1, L , #3). Читатель уже наверняка понял, что для каждой ячейки требуются две инструкции: одна указывает, что нужно делать, если считан символ 0, другая указывает, что нужно делать, если считан символ 1. Если в предыдущем примере третья инструкция указывает только действие, выполняемое в случае, если считан 0, но в действительности считан символ 1, то машина не сможет продолжить работу. Возможное решение этой проблемы может выглядеть так: в случае когда машина Тьюринга не имеет четких инструкций (а сама по себе она не способна «придумать», что делать дальше), она останавливается.

Чтобы сделать объяснение более понятным, укажем явно инструкции для всех возможных случаев. Рассмотрим очень простой пример с машиной Тьюринга Т , для которой заданы следующие три команды.

Инструкция № 1:Если считан 0, записать 1 и перейти к инструкции № 3.

Инструкция № 1:Если считан 1, сместиться вправо и перейти к инструкции № 2.

Инструкция № 2:Если считан 0, записать 1 и перейти к инструкции № 3.

Инструкция № 2:Если считан 1, остановить выполнение.

Инструкция № 3:Если считан 0, записать 1 и перейти к инструкции № 1.

Инструкция № 3:Если считан 1, остановить выполнение.

При кодировании машины Тьюринга согласно описанной системе возникает вопрос: что делать, когда машина останавливается? Ведь в этом случае не указано, какая инструкция должна быть следующей. Простейшим решением будет приписать символ 0: это гарантирует отсутствие ошибок, так как машина Тьюринга попытается найти инструкцию 0, но ни одна из инструкций не обозначена этим числом. Применив этот прием, запишем следующую последовательность инструкций, полностью описывающих работу Т :

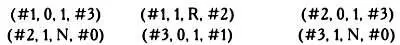
Теперь посмотрим, как будет действовать машина, если на ее вход подать ленту, на которой записаны только нули. Стрелка указывает положение считывающей головки машины Тьюринга в каждый момент времени.

Программа начинает выполнение первой инструкции. Так как считан 0, а инструкция гласит «Если считан 0, записать 1 и перейти к инструкции № 3», достаточно заменить 0 на 1 и посмотреть, как звучит третья инструкция.

Инструкция № 3 состоит из двух частей: первая указывает, что если считан 0, то нужно записать 1 и вернуться к инструкции № 1, однако согласно второй части этой инструкции, если считан символ 1, машина Тьюринга должна остановить работу. Так как в этом случае считан именно символ 1, программа прекращает выполнение. Следовательно, если подать на вход машины Тьюринга ленту, заполненную нулями, Т остановится после того, как запишет 1 в исходной точке.

Рассмотрим, что произойдет, если мы снова подадим на вход программы ленту, которую только что получили. Входные значения будут выглядеть так.

Начнем с первой инструкции: так как считан символ 1, нужно сместиться вправо и перейти к инструкции № 2. Никакой загадки нет.

Теперь, согласно инструкции № 2, если считан 0, машина Тьюринга должна заменить его на 1 и перейти к инструкции № 3. Последуем этой инструкции.

И вновь, согласно инструкции № 3, машина Т должна остановиться, если считан 1, следовательно, программа прекратит выполнение, а результатом ее работы будет лента, на которой записаны две единицы посреди бесконечного множества нулей, при этом устройство чтения-записи будет располагаться рядом с единицей, записанной справа. Если мы вновь запустим эту машину Тьюринга, в результате получим ленту, на которой будет записано три единицы, таким образом Т вычисляет не что иное, как значение функции f( n ) = n + 1. В общем случае функция является вычислимой, если существует машина Тьюринга, вычисляющая каждое из ее значений.