Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

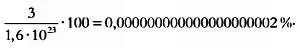
Неужели с этим смехотворным количеством информации мы можем прогнозировать состояние содержимого бутылки в каждый последующий момент? Хотя это и кажется невероятным, но это так.

Чтобы понять, каким образом мы это делаем, рассмотрим, какую информацию о внутреннем состоянии газа дают нам его давление, объем и температура.

Объем указывает нам, в какой области пространства находятся наши молекулы: нет ни одной молекулы кислорода вне бутылки, что помогает нам ограничить точки фазового пространства, в которых может находиться наш газ. Мы знаем, что возможные положения ограничены объемом сосуда. Понять роль, которую играет давление, несколько сложнее. Давление газа — это сила, которую он оказывает на сосуд, содержащий его, на единицу площади.

Представим себе, что газ — это джинн, заточенный в лампе. Чем меньше лампа и чем больше джинн борется за освобождение, тем большее давление он применяет. Чем больше давление, тем сложнее сдерживать газ; и если оно превысит определенные показатели, сосуд лопнет.

Но как связано давление с частицами, образующими газ? Если это вещество образовано огромным числом молекул, которые движутся хаотично, как объяснить эту силу, воздействующую на стенки сосуда? Давление — это результат совокупного действия миллионов молекул газа. Каждая молекула движется приблизительно по прямой до столкновения со стенкой; накопление этих столкновений и вызывает давление. Каждое столкновение воздействует на сосуд с определенной силой, и хотя удар одной молекулы не дает ощутимого эффекта, сотни миллионов молекул способны создать значительную силу.

Чем быстрее движутся молекулы, тем выше давление на стенки сосуда — по той же причине, что удар мячом по лицу тем болезненнее, чем быстрее летит мяч. Кроме того, чем больше молекул, тем большее давление они оказывают, поскольку в этом случае число ударов о стенки сосуда больше. Итак, давление дает нам информацию о движении частиц и об их числе, но в неполной форме: например, две частицы, сталкивающиеся со стенкой на одной и той же скорости, оказывают на нее такую же силу, как и две частицы на разных скоростях, если их средняя скорость равна скорости двух предыдущих частиц. Давление дает нам информацию о средней скорости частиц газа, но ничего не говорит о скорости каждой конкретной частицы.

Последняя часть информации, которой мы владеем, — это температура газа. Природа температуры была загадкой в течение веков, когда думали, что она связана с количеством флюида под названием теплород, содержащегося в веществе. Сегодня мы знаем, что температуры самой по себе не существует, то есть в фундаментальных законах Вселенной нет ничего, что было бы связано с температурой. Когда мы дотрагиваемся до очень горячего объекта, то на самом деле мы чувствуем движение частиц, его образующих. Повышенная температура соответствует быстрому движению, а низкая температура — более медленному движению. Понятие температуры можно будет определить точнее, как только мы раскроем математические инструменты, позволяющие изучать газ на основе его микроскопических характеристик. Мы можем утверждать, что температура показывает нам, как движутся молекулы. Если мы знаем температуру, объем и давление газа, то можем выяснить и сколько в нем примерно молекул и с какой средней скоростью они движутся.

* * *

ЗАКОН ИДЕАЛЬНОГО ГАЗА

Газ образован электрически заряженными молекулами разнообразных форм, и именно по этой причине так сложно предсказать их поведение. К счастью, при высоких температурах и низких давлениях эти молекулы ведут себя практически как идеально круглые мячи, которые взаимодействуют только при столкновении друг с другом. Газ, образованный таким типом частиц, называется идеальным газом, и его поведение можно описать простым уравнением.

Уже в XVII веке открыли, что произведение давления на объем газа остается постоянным при постоянной температуре. Также было известно, что повышение температуры влечет за собой повышение давления при постоянном объеме или увеличение объема при постоянном давлении. Количество газа также имеет значение: чем больше молекул, тем больше давление, так как число столкновений со стенками сосуда растет.

Все эти открытия можно свести воедино в известном законе идеального газа. В формуле ниже Робозначает давление, V— объем, Т— температуру, R — газовую постоянную, а n — это величина, связанная с числом молекул:

PV= nRT.

С помощью этого простого уравнения можно объяснить большую часть свойств газов, которые мы наблюдаем.

* * *

Зная объем, температуру и давление газа, мы не можем знать, в какой части фазового пространства он находится, но можем ограничить область, в которой микроскопические свойства порождают макроскопические, которые мы и наблюдаем. Для этого сначала рассмотрим две частицы, чтобы затем расширить наш метод на сколь угодно большое их число. Также ограничимся только одним измерением, то есть предположим, что частицы движутся стихийно из стороны в сторону по прямой, что позволит увидеть их положения в фазовом пространстве.

Предположим, что наши частицы ограничены областью пространства длиной в один метр, то есть представим, что газ находится в коробке объемом в один кубический метр. Вне этой области частицы находиться не могут. Если мы обозначим через q 1 положение первой частицы и через q 2 — положение второй, их общее положение в фазовом пространстве будет ограничено квадратом со стороной в метр, как показано на рисунке.

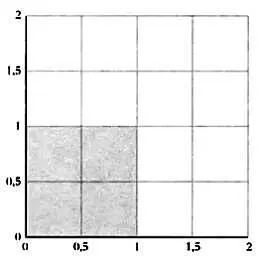
То есть ни частица 1, ни частица 2 не могут выйти за пределы области, их ограничивающей.

Поскольку мы знаем температуру и давление частиц, мы также знаем, чему равна их средняя скорость. Чтобы вычислить ее, сложим скорость обеих частиц и разделим ее на два. Выражаясь математически, если v¯ обозначает среднюю скорость, v 1 — скорость первой частицы, a v 2 — скорость второй, получается, что:

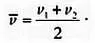
Для N частиц мы бы сложили скорости их всех и разделили на N , то есть

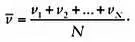
Мы считаем, что все скорости положительны и все частицы движутся в одном направлении. Теперь предположим, что средняя скорость обеих частиц — 2 м/с. Может быть так, что обе движутся со скоростью 2 м/с; что одна движется со скоростью 3 м/с, а другая — 1 м/с; что одна абсолютно неподвижна, а другая движется со скоростью 4 м/с. Единственный невозможный вариант — так это чтобы какая-либо из двух частиц двигалась со скоростью больше 4 м/с, поскольку тогда средняя скорость была бы больше 2.