Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

Другой способ применения динамических систем связан с нейробиологией, где нелинейная природа процессов в нашем мозге превращает эти системы в инструмент, необходимый для изучения как индивидуального поведения нейронов, так и общей структуры мозга. Эти модели можно применять для построения новых моделей, что, в свою очередь, ведет к прогрессу в области создания искусственного интеллекта. Действительно, нейронные сети, используемые такими программами, как Siri или распознавание голоса от Google , могут рассматриваться как тип динамической системы. Более подробно они будут рассмотрены в главе 5.

Молекулярная биология также воспользовалась преимуществами, которые дают динамические системы при моделировании взаимодействия между протеинами или механизмов клеточной пролиферации. Очень интересный способ применения — это использование динамических систем для прогноза роста опухолей, что позволяет более точно определять размер и расположение новообразований, повысить эффективность лечения и избежать неприцельного использования рентгенотерапии. Также очень большую роль динамические системы сыграли в экологии, где они используются для описания поведения пищевых цепочек различных видов и для прогнозирования изобилия в определенных областях, а также для изучения эффекта введения в экосистему определенного числа хищников. Анализируя траектории изменения системы, можно установить сферу наименьшего поражения в каком-либо регионе или даже определить стратегии, позволяющие избежать вымирания вида и решить другие проблемы, связанные с окружающей средой.

В социальных науках особую пользу из теории динамических систем извлекает экономика. Бенуа Мандельброт(1924–2010) открыл, что цены на хлопок колеблются, следуя хаотической структуре, сходной на всех уровнях: то есть вне зависимости от периода времени, который берется в расчет, от десяти минут до десяти лет, цены на хлопок показывали один и тот же тип колебаний. Это типичная характеристика хаотических систем, что делает их подходящими для изучения подобных ситуаций.

Так же, как и в физике, многие математические инструменты, используемые для анализа развития экономики, связаны с состоянием равновесия — условием, необходимым для формулирования математически управляемой теории. Использование динамических систем позволяет ослабить это условие и работать с системами, меняющимися со временем.

Наконец, некоторым авторам, таким как Кэтрин Эннис, профессор кинезиологии в Мэрилендском университете, удалось использовать инструменты, основанные на динамических системах, для моделирования образовательного процесса.

Динамические системы применяются очень широко и постоянно появляются новые области их применения, особенно в сферах, традиционно мало связанных с математикой (например, в биологии). Во многих дисциплинах этот мощный инструмент сделал возможными количественные исследования там, где раньше существовало только качественное понимание. Наверняка в следующие десятилетия использование динамических систем еще более расширится, особенно в таких науках, как социология.

Динамические системы — идеальный пример того, как развивается математика: от описания физической системы она приходит к более абстрактной и общей формулировке, которая затем распространяется на большее количество областей, совсем не связанных с первоначальной сферой. Как мы увидим, история повторится и с остальными инструментами, необходимыми для изучения такого явления, как поведение газов.

Газ — это агрегатное состояние, представляющее собой тысячи миллионов молекул, которые движутся хаотично. Поскольку каждая молекула подчиняется законам Ньютона и, соответственно, уравнениям Гамильтона, можно было бы рассчитать траекторию каждой из них. Но на практике это не так. Более того, в таких вычислениях нет необходимости, потому что при наблюдении газа невозможно увидеть отдельные молекулы. Что действительно можно измерить, так это его давление, температуру и объем. Следовательно, математическая теория, описывающая изменение этих трех характеристик, смогла бы с достаточной степенью точности описать и поведение газа.

Такая теория была разработана австрийским физиком Людвигом Больцманом в конце XIX века, когда он доказал, что макроскопические характеристики газа можно вывести исходя из распределения скоростей его молекул. То есть достаточно знать процент молекул газа с каждой возможной скоростью, чтобы предсказать его поведение. Работа Больцмана была направлена на то, чтобы найти это распределение скоростей для газа в состоянии равновесия, то есть газов, макроскопические свойства которых ощутимым образом не изменяются. Ученый открыл, что скорости молекул в газе распределяются следующим образом.

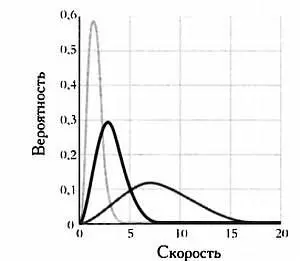
Газ с большим пиком слева соответствует большим температурам.

Чтобы сделать это, ему пришлось воспользоваться несколькими математическими теориями. Одни из них, такие как механика Гамильтона, были хорошо приняты в физическом сообществе, но другие, такие как вероятность и статистика, были совершенно новыми. Ниже мы опишем путь, который привел Больцмана к его закону и математическому обоснованию предыдущего графика.

Вспомним, что состояние системы в определенный момент времени может быть выражено лишь одной точкой в фазовом пространстве. Эта точка находится в пространстве из 6 N измерений, где 3 N используются для уточнения положения каждой из N частиц, а другие 3 N — для импульсов. Если позволить системе развиваться, точка будет двигаться по фазовому пространству, описывая некоторую траекторию.

В случае с газом в самом начале мы сталкиваемся с проблемой: мы не знаем, в какой точке фазового пространства он находится. Мы знаем только его давление, объем и температуру, но не положение и не импульс его частиц. Часто мы даже не можем быть уверены в том, сколько их. Как же получить какой-либо прогноз поведения системы, о которой мы знаем так мало?

Для начала оценим наше незнание количественно: возьмем бутылку, наполненную кислородом. Если вместимость бутылки — один литр, то в ней содержится приблизительно 2,6·10 22молекул, что означает, что для того, чтобы полностью описать их состояние, нам потребуется это количество чисел, умноженное на шесть, то есть 1,6·10 23(2,6·10 22·6 ~= 1,6·10 23). Предположим, что мы знаем температуру, объем и давление газа, то есть у нас есть три характеристики. Таким образом процент информации, которой мы владеем, в сравнении с информацией, теоретически нам необходимой, равен: