Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

* * *

Типичный пример — горячий лед, который можно сделать на кухне. Смешаем уксус с пищевой содой и получим ацетат натрия. Затем из кипящей воды и соли получим перенасыщенный раствор, добавим в него немного ацетата, и он закристаллизуется.

Если поставить раствор в холодильник, его температура снизится, будет пройдена граница точки замерзания, после которой состояние вещества с минимальной энергией должно быть твердым, но не жидким. Однако наш раствор все еще остается в жидком состоянии, а чтобы перейти в твердое, ему нужна некоторая энергия. Слегка постучим по стакану пальцем. Раствор получит достаточную энергию, чтобы дойти до реального минимума. При этом вся лишняя энергия высвободится, превращаясь в тепло. Мы увидим сверхскоростную реакцию, при которой раствор за несколько секунд застывает с высвобождением большого количества энергии, которая согревает получающийся кристалл. Наш раствор стал похожим на лед, но этот лед будет горячим.

Решить уравнения Гамильтона для газа невозможно, но по крайней мере мы знаем, что газ ведет себя как динамическая система. Следовательно, у него будут те же характеристики, что и у обычной динамической системы, и вывести их можно с помощью элементарной математики и здравого смысла. Вспомним, что теория динамических систем — это не физическая, а математическая теория: любая система, изменяющаяся во времени по определенному правилу, — динамическая.

Мы можем представить газ как одну частицу, движущуюся в двух измерениях и описывающую некоторую траекторию. Конечно, движение газа сложнее, но качественные характеристики примерно такие же.

Если взять динамическую систему и начать вычислять ее траектории исходя из различных начальных условий, мы получим рисунок, похожий на приведенный ниже.

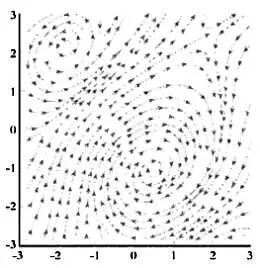
Это говорит о том, что несмотря на сложное поведение, такие динамические системы, как газ вне состояния равновесия, демонстрируют некоторые закономерности, которые можно определить, изучив траектории. Если мы обратим внимание на рисунок, то увидим, что наша система стремится приблизиться к некоторым областям фазового пространства. Эти области называются аттракторами, они бывают различных типов, с разными характеристиками. Если предоставить динамической системе для изменения достаточно времени, любая из них будет стремиться к аттрактору, поскольку все траектории ведут к ним.

Аттрактор необязательно должен быть точкой: это в целом область фазового пространства, которая может быть точкой, плоскостью, некоторым объемом или даже иметь более сложную форму.

Самый простой вид аттракторов — это неподвижная точка, или точка в фазовом пространстве. Если динамическая система находится в этом аттракторе, она из него никуда не передвинется. Вспомним, что динамическая система связана с трансформацией, переходом из одной точки фазового пространства в другую, но если аттрактор — неподвижная точка, то любые трансформации приводят нас в нее же.

Пример такого аттрактора — самое нижнее положение качелей: если человек находится в этой точке, он в ней и останется, если только не будет применять силу. И наоборот, находясь вверху, он стремится к этой нижней точке (это и указывает, что речь идет об аттракторе).

Но аттракторами являются не все неподвижные точки. Мяч на вершине горы представляет собой другую неподвижную точку — репульсор: минимальное воздействие вызовет перемещение мяча от нее. Итак, неподвижные точки, являющиеся аттракторами, совпадают с системами в стабильном равновесии, в то время как неподвижные точки, являющиеся репульсорами, показывают нам, что система находится в состоянии нестабильного равновесия.

Один из самых интересных видов аттракторов — это предельный цикл, или периодическое движение, к которому стремится система, если располагает достаточным количеством времени.

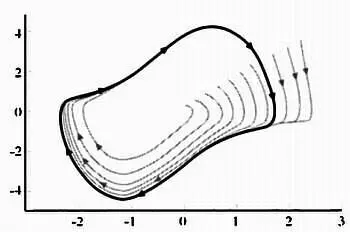
Пример предельного цикла. Все траектории стремятся к форме пути, выделенному жирным.

Как можно заметить, любая соседняя орбита предельного цикла стремится к нему. Классический пример предельного цикла — часы с маятником, период колебания которого определен длиной маятника, а дополнительная энергия исходит от гири и от завода часов. Обычный маятник, однако, стремится потерять энергию и остановиться в точке стабильного равновесия. Предельные циклы возникают только в системах с постоянным притоком энергии, как в случае с земной атмосферой.

Предельные циклы замечены во всех видах систем. Наиболее интересный случай — химические часы, о которых далее мы расскажем подробнее: в них два вещества реагируют друг с другом, и одно способно превращаться в другое. В некоторых условиях оба вещества превращаются друг в друга с определенным периодом, который можно видеть невооруженным глазом по смене цвета раствора.

Еще сложнее, чем предельные циклы, странные аттракторы. В этом случае траектории стремятся к области с фрактальной структурой. Фрактал — это геометрическая фигура, которая обладает самоподобием, то есть любая часть фрактала подобна ему целиком. Классический пример — снежинка Коха.

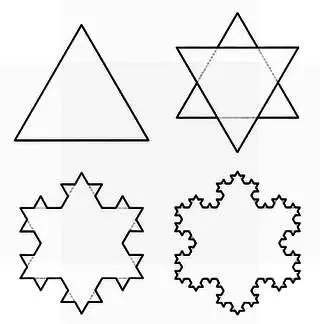
Различные этапы создания снежинки Коха.

Конечная фигура получается в результате бесконечного числа этапов.

Эту фигуру можно построить, применяя одну и ту же трансформацию несколько раз для каждой линии рисунка, так что он усложняется с каждым циклом. Трансформация применяется бесконечное число раз, и это предполагает, что фигура имеет одинаковый вид, в каком бы масштабе мы на нее ни смотрели. На рисунке слева на следующей странице показано множество Мандельброта — одна из самых известных фрактальных структур, в определенном масштабе, а справа — тот же самый фрактал, увеличенный в 100 раз.

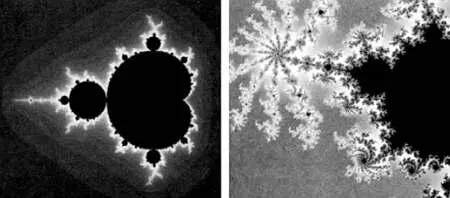
Фракталы имеют дробную размерность, то есть для них характерно не целочисленное количество измерений — одно, два или три, — а, например, 1,65. Это можно объяснить следующим образом: если вычислить периметр снежинки Коха, окажется, что он бесконечен, потому что линии фигуры бесконечно сложны. Итак, с одной стороны, определяющая его линия имеет больше одного измерения, значит, ее размерность должна лежать в промежутке между единицей и двумя. Существуют различные способы вычислить размерность фрактала, и в случае со снежинкой она примерно равна 1,26.