Хоакин Наварро - Том 31. Тайная жизнь чисел. Любопытные разделы математики

Математики-любители вызывают определенное восхищение у простых людей. Любители редко получают свои удивительные знания обычным путем и часто отличаются необычными способностями, как, например, польский математик Стефан Банах(1892–1945) или индиец Сриниваса Рамануджан — это лишь два примера ученых, не имевших классического образования, но занявших место на математическом Олимпе. Однако королем среди любителей был Пьер Ферма(1601–1665) — юрист, читавший книги по арифметике, поля которых были слишком узки для его поистине чудесных доказательств.

Прекрасным примером ученого-самоучки является также Джордж Грин(1793–1841) , который совершенно самостоятельно прошел путь к математической мудрости. Он обладал одним странным для британца качеством: в его время в Англии считалось дурным тоном использовать в математическом анализе нотацию Лейбница вместо нотации Ньютона. Однако Грин мало оглядывался на общественное научное мнение и малопонятной нотации Ньютона предпочитал способ записи Лейбница. Такая независимость его мышления удивляет еще больше, если учесть, что он был простым мельником. Грин, сын разбогатевшего пекаря, до 40 лет не осмеливался поступить в Кембридж, и его насилу удалось уговорить. Именно благодаря его трудам сегодня нам известна теорема Грина (она также независимо от него была сформулирована русским математиком Михаилом Остроградским(1801–1861)) , влияние которой прослеживается даже в современном дифференциальном и интегральном исчислении:

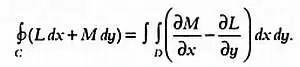
Работы Грина позднее позволили ученым добиться значительных успехов даже в квантовой механике — науке, совершенно немыслимой в XIX веке. Из «Небесной механики» Лапласа Грин вывел вполне достойную математическую теорию электричества. В последние годы жизни он часто прикладывался к бутылке. Словом, этот мельник — сегодня в его мельнице находится музей — в обычной жизни, скорее всего, был совершенно простым и довольно приятным человеком.

Одним из результатов практического применения теоремы Гринастало создание планиметра — прибора, позволяющего определить площадь замкнутой фигуры неправильной формы.

Бельгийский физик Жозеф Плато (1801–1883) был большим экспериментатором и получил множество результатов, описывающих персистенцию зрения и принцип действия сетчатки глаза. Он же изобрел фенакистископ. Сегодня изобретения Плато и их производные отошли в область занимательной физики, хотя именно благодаря им стало возможным изобретение кинематографа.

Фенакистископ стал первым прибором, в котором использовалась персистенция — способность глаза запоминать последовательные события. При вращении диска кажется, что фигуры движутся.

Но как это связано с математикой? Плато почти случайно провел эксперименты с маслянистыми жидкостями, в итоге которых родилась теория, описывающая поверхностное натяжение и форму мыльных пленок. Если погрузить криволинейную структуру, представляющую собой контур поверхности (например, изогнутую проволоку), в мыльную пену, то образуется пленка, которая будет поверхностью наименьшей площади, а границей этой поверхности станет проволока. Именно здесь в игру вступает математика: вычислить поверхность наименьшей площади математическими методами — с помощью вариационного исчисления, частных производных высших порядков и так далее — очень сложно или даже невозможно. Чтобы найти физическое решение, достаточно воды и мыла. Таков весьма достойный вклад Плато в математику.

Поверхность наименьшей площади, заключенная между двумя дугами, — это не прямой цилиндр, а катеноид, что доказывает эксперимент с мыльными пленками, изображенный на фотографии.

Жизненный путь Плато полон казусов. В 1829 году ученый наблюдал Солнце невооруженным глазом в течение 25 секунд и ослеп. Этот эксперимент был абсолютной глупостью, и Плато вошел в историю как человек, принесший в жертву науке свое зрение. Согласно более реалистичной версии, экспериментатор ослеп лишь частично, потом его зрение восстановилось, но спустя некоторое время, в 1843 году, он вновь начал терять зрение, в этот раз по неясным причинам, и до самой смерти продолжал научную работу в кромешной тьме.

Планета Нептун была открыта в 1846 году, и это стало триумфом математических методов вычислений. Можно сказать, что само открытие было совершено задом наперед. Началось все с наблюдения за Ураном — планета все время отклонялась от расчетной орбиты, и объяснить это можно было воздействием на нее неизвестного небесного тела. В истории об открытии Нептуна лицом к лицу сошлись английские и французские ученые, и конфликт выплеснулся далеко за пределы Англии и Франции — поговаривали, что уважаемые мудрецы таскали друг друга за бороды, а серьезные журналы публиковали подстрекательские статьи. Открытие Нептуна приписывается главе Парижской обсерватории Урбену Жану Жозефу Леверье(1811–1877) и юному английскому астроному Джону Кучу Адамсу(1819–1892) .

Изначально посчитали, что именно Леверье принадлежит честь открытия Нептуна, а все притязания Адамса — просто подозрительная инсинуация, однако позднее историки подтвердили, что Адамс опередил именитого французского коллегу. Ученые сделали свои открытия независимо друг от друга, их труды были выполнены на самом высоком уровне и содержали обширнейшие и сложнейшие расчеты.

Истории уже известен случай, когда между Англией и Францией разгорелась бескровная война относительно того, кто же был истинным автором математического анализа — Ньютон или Лейбниц. Спор между Леверье и Адамсом стал повторением этого конфликта. В обоих случаях причины для дискуссии отсутствовали, однако жаркие споры, несомненно, куда интереснее объективных поисков истины.

Наиболее забавным эпизодом этой истории стали притязания Леверье: со слов Франсуа Араго(1786–1853) , астроном хотел назвать новую планету своим именем, о чем заявил на заседании Французской академии наук. Не стоит и упоминать, что это предложение было отвергнуто почти единогласно, и, как ни настаивали французские ученые, новая планета получила имя древнегреческого бога Нептуна. Сегодня ее символ — стилизованный трезубец.