Хоакин Наварро - Том 31. Тайная жизнь чисел. Любопытные разделы математики

В 1966 году ученый был удостоен Филдсовской премии, но отказался ее принять. В 1988 году ему была присуждена престижная премия Крафорда — аналог Нобелевской премии в дисциплинах, где эта премия не присуждается. Гротендик отказался и от нее. Золотые годы он провел в Институте высших научных исследований близ Парижа и покинул его, едва узнал, что финансирование частично предоставлялось источниками, близкими к вооруженным силам. Один из докторантов Гротендика, Пьер Делинь(род. 1944) в 1978 году был также удостоен Филдсовской премии.

Позднее были опубликованы остросюжетные, хотя и весьма путаные воспоминания ученого, а также несколько его трудов. Все эти книги отличались внушительными размерами. Он редко вступал в личный контакт, предпочитая переписку. Уже более 20 лет нам ничего неизвестно о его новых работах, и нет надежды, что имя Гротендика когда-нибудь промелькнет в новостях — разве что по случаю его кончины. Как жаль, что мы лишились такого ученого!

Как вы уже знаете, некоторые правители, к примеру Наполеон или Имон де Валера, испытывали любовь к математике. Например, экс-президент США Джеймс Гарфилд(1831–1881) во время одного из скучнейших заседаний даже нашел новое доказательство теоремы Пифагора. Однако существуют и политики, взаимоотношения которых с математикой не столь успешны. Известна очень смешная история о Тони Блэре, рассказанная учителем математики в Chorister School , где юный Блэр учился. В ответе к задаче о прямоугольных треугольниках он почему-то упомянул слово «носорог». Блэр признался, что использовал это слово по уважительной причине: «Я бы написал "гиппопотам", но не был уверен, как именно оно пишется, поэтому не захотел огорчать учителя и написал первое более или менее похожее слово, которое пришло в голову». Словом, которое никак не мог вспомнить Блэр, была «гипотенуза». В этот момент Евклид, наверное, перевернулся в гробу.

Путаница между словами «гиппопотам» (англ, hippopotamus ) и «гипотенуза» (англ, hypotenuse ) стала классической темой математических анекдотов. Мы привели здесь эту историю потому, что она подтверждена документально и в ней рассказывается об известной личности.

Как сказал бы капитан Хэддок, друг героя комиксов Тинтина, у всех бутылок в нашем мире есть «внутри» и «снаружи», и они либо пусты, либо в них что-то налито. Но правильнее было бы сказать «почти у всех», поскольку существуют математические бутылки (бесполезные для Хэддока и потому ему неизвестные), обладающие весьма необычными свойствами. Немецкий математик Феликс Клейн(1849–1925) в 1882 году описал бутылку, у которой, как вы можете видеть, нет ни внутренней, ни наружной части. И выпить из нее нельзя.

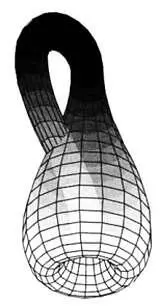
Читатель, конечно, может попытаться представить ее себе полной или пустой, но в нашей трехмерной Вселенной такая бутылка, к несчастью, пронзает сама себя, а вот в четырехмерном пространстве — вполне возможна. Со строго геометрической точки зрения, бутылка Клейна — это замкнутая неориентируемая поверхность без границы, которая изучается в топологии наряду со своей сестрой, лентой Мёбиуса.

Анекдотичность этой геометрической диковинки заключена в ее названии, куда вкралась ошибка: изначально на немецком языке бутылка Клейна называлась Kleinsche Flache , то есть «поверхность Клейна». Если кто-то хочет изобразить эту поверхность (для этого достаточно компьютерной программы и принтера), он должен будет построить график следующего уравнения в декартовых координатах:

( x 2 + у 2+ z 2+ 2 у — 1)·[( x 2+ у 2+ z 2— 2 y — 1) 2 — 8 z 2] + 16 xz ( x 2+ y 2+ z 2— 2 y — 1) = 0

Однако даже математики порой ошибаются, и Kleinsche Flache стало писаться как Kleinsche Flasche , что как раз и означает «бутылка Клейна». А поскольку слово «бутылка» тоже довольно точно описывает поверхность Клейна, то это ошибочное название стало в научном мире общепринятым.

Открытие бутылки Клейна предоставило ряд возможностей и для бизнеса: в интернете вы найдете шапки, имеющие форму поверхности Клейна, или ковши для зачерпывания вина, которые представляют собой практически ее копию.

Процитированные выше строки взяты из памфлета «Аналитик» ( The Analyst , 1734) — прекрасного интеллектуального упражнения англиканского епископа, посвященного «одному неверующему математику» — по-видимому, Беркли имел в виду Эдмунда Галлея(1656–1742) , который славился своей недоверчивостью.

В памфлете Беркли выступает против недавно появившегося ньютоновского исчисления, столь обожаемого Галлеем и всем научным миром, возражая им (и небезосновательно), что если они не верят в Бога, поскольку священные тексты им непонятны, то не следует верить и в почти мистические хитросплетения математического анализа.

Прошли годы и даже столетия, доверие к математическому анализу было восстановлено благодаря более строгим и четким, но менее интуитивным определениям. Тем не менее не стоит забывать слова Беркли, превосходного философа-эмпирика (его именем назван знаменитый американский университет). Напротив, следует отдать ему дань уважения за грамотную и обоснованную критику.

Методы, описанные Ньютоном и Лейбницем, открыли множество путей в науке и вместе с тем породили множество анекдотичных ситуаций. Приведем некоторые из них.

Портрет епископа Джорджа Беркликисти Джона Смайберта.

Очевидно, что гипотеза и теорема — не одно и то же. Гипотеза обретает статус теоремы только после доказательства, однако довольно долго это не учитывалось.

Рассмотрим, например, труды Иоганна Кеплера(1571–1630) . Все мы не раз почтительно отзывались о его законах, которые представляют собой эмпирические выводы, основанные на таблицах Тихо Браге(1546–1601) . Эти законы можно назвать гениальными, они широко известны в научном мире и точно описывают движение небесных тел, хотя для них не приводится какого-либо математического доказательства. Сегодня, с вершин нашего знания, можно сказать, что это были три блестящие гипотезы, но не три теоремы.