Хоакин Наварро - Том 31. Тайная жизнь чисел. Любопытные разделы математики

3. Единодушие: если все выбирают какой-то вариант, он является окончательным.

4. Единственность: результат голосования всегда будет одним и тем же, если предпочтения избирателей не меняются.

5. Независимость незначащих альтернатив: если исключить из голосования один вариант, остальные не изменятся.

Лауреат Нобелевской премии по экономике 1972 года Кеннет Эрроу(род. 1921) подробно изучил вышесказанные характеристики с точки зрения математики и вынес удивительный вердикт: не существует системы голосования, которая соответствовала бы всем указанным условиям. Она может соответствовать некоторым

из них, но не всем одновременно. «У каждого свои недостатки», как говорил герой

Билли Уайлдера в фильме «В джазе только девушки».

Американский математик Ив Нивергельт был автором работ о компьютерах, вейвлетах и статистике. Одна из его статей, опубликованная в 1987 году, стала настоящим бестселлером среди студентов, изучающих экономику и социологию. В ней, в частности, идет речь о математическом понятии эластичности.

Непосвященный напрасно будет пытаться понять, в чем же заключено очарование этой статьи: она полна формул с производными, логарифмами и другими математическими ужасами. Если вы прочитаете статью до конца, то узнаете, что курить — вредно, а антитабачные пошлины почти не влияют на курильщиков, однако позволяют выручить средства, которые затем направляются на борьбу с курением.

Также в статье рассказывается, что спрос на лосося, помимо прочих факторов, зависит от его относительной численности, от выживаемости икринок и молодых особей и так далее. Словом, вы узнаете много интересного о самых разных явлениях.

Если какую-то игру и можно назвать царицей игр, то этого титула, несомненно, заслуживают шахматы. В них случайность никак не влияет на ход игры, а определяющее значение имеют чистая стратегия и память: число возможных ходов в партии имеет порядок 10 123— это невообразимая величина. Однажды чемпионом мира по шахматам стал профессиональный математик Эмануэль Ласкер(1868–1941) .

Сейчас мы говорим о стандартных шахматах на доске из 64 клеток, но еще в далекую викторианскую эпоху математик Артур Кэли(1821–1895) уже рассмотрел трехмерные шахматы, в которые сегодня играют персонажи сериала «Звездный путь».

Пока что никто не смог должным образом изучить эту игру — она слишком сложна даже для передовых методов современной теории игр. Но существует несколько ценных результатов: испанский инженер Леонардо Торрес Кеведо(1852–1936) в 1914 году сконструировал шахматный автомат, который всегда одерживал победу в окончании шахматной партии для трех фигур (король против короля и ладьи). Конечно, мы по-прежнему далеки от заветной цели — алгоритма, указывающего путь к победе в любой партии, но надо же с чего-то начать.

Машина под названием «Турок», сконструированная венгерским инженером Вольфгангом фон Кемпеленомв 1769 году, произвела фурор. Казалось, что машина способна играть в шахматы, однако на самом деле она была искусной фальшивкой — внутри механизма прятался человек.

Шахматы — прекрасное поле битвы, можно даже сказать, первой битвы в вечном противостоянии человека и машины. Известно, что шахматные программы становятся все совершеннее, и сложно устоять перед соблазном столкнуть лицом к лицу гроссмейстера и такую программу. В 1996 году уже состоялся поединок между компьютером Deep Blue, созданным компанией IBM, и чемпионом мира по шахматам Гарри Каспаровым. Каспаров выиграл со счетом 3:0. Таким образом, в 1996 году человек опередил машину.

На следующий год программное обеспечение Deep Blue было улучшено, и поединок прошел вновь. Теперь машина одержала верх. Каспаров остался не слишком доволен результатом и предположил, что во время партии в действия компьютера вмешивался человек. Компания IBM, как и следовало ожидать, отвергла обвинения. Желаемая цель, отчасти пропагандистская, была достигнута, и после этого компьютер был разобран. В 2000 и 2003 годах прошли новые поединки между гроссмейстерами и компьютерами, сменившими Deep Blue, все они завершились ничьими. Вероятно, в будущем мы увидим новые партии между человеком и машиной.

В конце концов люди запомнят только одно: благодаря техническому прогрессу машина одержала верх над человеком — рано или поздно это все равно произойдет. Однако по-настоящему важен ответ на другой вопрос: подобно ли мышление человека мышлению машины? Этого мы пока не знаем. Быть может, мы не узнаем этого вообще никогда, и вопрос останется гёделевским утверждением, дать ответ на которое невозможно.

Deep Blue— первый шахматный компьютер, одержавший верх над чемпионом мира.

Математики прошлого очень отличаются от современных ученых и, безусловно, заслуживают большого уважения и почитания. Рассуждали они не так, как мы, им были неизвестны эффективные и универсальные обозначения, у них не было научных журналов и интернета, на распространение новых идей в то время в лучшем случае уходили десятилетия, и окружающие очень часто считали ученых чудаками. Проходили столетия, и сегодня математики — люди высшего разума. Но и в самые далекие времена математики были необычными существами, невероятно одаренными и удивительно мудрыми.

Одним из семи греческих мудрецов, по мнению Павсания, был Фалес Милетский (ок. 639 года до н. э. — ок. 547 года до н. э.) . Он занимался самыми разными науками, но мы считаем его математиком, поскольку, согласно Евклиду, Фалес первым доказал некоторые геометрические утверждения — сегодня они кажутся нам примитивными, но в свое время вовсе не были таковыми. К примеру, именно Фалес первым сказал, что существует прямая, называемая диаметром, которая делит круг пополам, что углы, противолежащие равным сторонам равнобедренного треугольника, равны или что накрест лежащие углы равны. Не будем забывать и о теореме, носящей его имя, с помощью которой Фалес измерил высоту пирамиды, зная длину ее тени и длину тени посоха (как именно он это сделал, показано на иллюстрации).

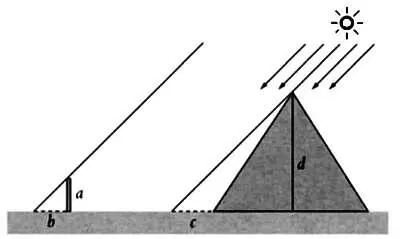
Применив теорему, носящую его имя, Фалесвычислил высоту d, зная высоту посоха аи длину теней bи с: d= a· c/ b