Альберт Виолант-и-Хольц - Том 9. Загадка Ферма. Трехвековой вызов математике

Благодаря новой организации работы, предложенной Мерсенном, к решению интересных задач приглашались все талантливые ученые. Найденные решения были не плодами труда одиночек-затворников, а, напротив, результатом взаимодействия и обмена идеями. История науки знает множество примеров, когда формулы и теории получали имя своих первооткрывателей. Но в этой новой среде достижения часто были результатом коллективного труда. Кто мог представить, что эта красивая кривая, которую впервые описал Галилей как движение точки окружности при качении вдоль прямой, спустя много лет окажется решением задачи о брахистохроне и таутохроне, и что Жерар Дезарг предложит придать зубцам часовых механизмов именно форму циклоиды!

Понте ди Меццов Пизе, спроектированный учениками Галилея. Его арки имеют форму циклоиды. Мост был разрушен в 1944 году.

Роберваль и Мерсенн заинтересовались результатами Ферма относительно максимумов и минимумов. Задачи, которые предлагал Ферма (равно как и ответы на них), были не случайны — при их решении использовались методы, неизвестные другим математикам той эпохи. Они поняли, что Ферма значительно опередил современников в решении задач о максимумах и минимумах, и попросили его объяснить методы, которые он использовал. Ответ не заставил себя долго ждать. Ферма отправил Мерсенну и Робервалю три текста («Методы нахождения максимумов и минимумов и построения касательных к кривым», «О плоских и телесных местах» и труд Аполлония «Плоские места» в двух книгах), чтобы их оценили парижские математики. Так Ферма стал известен как математик первой величины.

В своем «Методе максимумов и минимумов» Ферма отметил, что в точке максимума функции прямая, параллельная оси абсцисс, касается графика этой функции только в одной точке. Он также отметил, что в точках, очень близких к точке максимума, прямая, параллельная оси абсцисс, пересекает график этой функции в двух близких точках справа и слева от точки максимума.

Следовательно, значение функции в точке экстремума f( а ) и значение, очень близкое к нему, f( а + е ), где е — очень малая величина, практически одинаковы, следовательно, согласно Ферма, их можно «приравнять». В результате получим уравнение, исключив из которого величину е (так как она очень мала) мы сможем рассчитать а .

Рассмотрим пример. Пусть дана функция f( х ) = х 2. Ее график представлен на рисунке ниже.

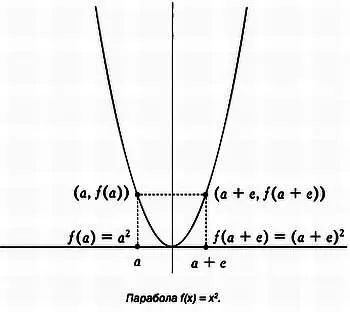
Пусть нужно вычислить минимум этой функции, f( а ) = а 2. Для этого рассмотрим значение, очень близкое к нему: f( а + е ) = ( а + е ) 2= а 2+ 2 ае + е 2. «Приравняем» их, то есть поставим между этими выражениями знак равенства: а 2= а 2 + 2 ае + е 2. На следующем шаге решим полученное уравнение. Вычтя а 2 из обеих частей равенства, получим 2 ае + е 2= 0, откуда, сократив на е , получим 2 а + е = 0.

Наконец, будем считать е столь близким к 0, что им можно пренебречь. Имеем 2 а = 0, следовательно, а = 0 — это корректная точка минимума данной функции.

Как можно видеть, после «приравнивания» мы получили уравнение, равносильное равенству нулю производной этой функции. Но в те времена не было известно ни о вычислении производных, ни о нахождении пределов функций. Поэтому не удивительно, что некоторые математики признавали этот метод лишь с оговорками. Но в этом случае Ферма проявил потрясающую интуицию. Он выглядел фокусником, который умело манипулирует алгебраическими выражениями и в итоге непостижимым образом получает желаемый результат.

Восстановление утерянных трудов Аполлония было частью амбициозного проекта, начатого Виетом и Марино Гетальди, к которым позднее присоединились Виллеброрд Снелл и сам Ферма, высоко ценивший Аполлония. Кроме этого, Ферма был великолепным знатоком античных языков, а благодаря знаниям математики с удивительной легкостью справился бы со сложной задачей перевести труды античных авторов с латыни и греческого. Поэтому неудивительно, что переводчики, работавшие со сложными научными текстами, обращались к нему за советом.

В Тулузе Ферма познакомился с Шарлем де Моншалем, специалистом по древнегреческому языку и большим библиофилом, чья коллекция рукописей впоследствии составила часть Королевской библиотеки. Ферма получил доступ к этому удивительному собранию. Моншаль продемонстрировал ему Les harmoniques — книгу о музыке, написанную византийским автором XIV века. Ферма прочитал ее и сделал несколько пометок на полях в своем стиле: когда он читал, то давал простор воображению, у него возникало множество идей, и он записывал их, чтобы вернуться к ним позже.

В Кастре он познакомился с Пьером Сапорта, который в 1664 году написал «Трактат об измерении текущей воды» ( Traité sur la mesure des eaux courantes ) — перевод на французский язык книги бенедиктинского священника Бенедетто Кастелли.

Он также перевел на французский одну из работ Торричелли на ту же тему. Кроме того, Сапорта решил включить в свой перевод описание инструмента для измерения плотности жидкостей, которое написал Ферма. Этот инструмент впервые описал Синезий, епископ из Кирены, современник Гипатии Александрийской. Тот же Кастелли указал, что до Ферма многие безуспешно пытались понять принцип действия этого устройства. Сапорта ценил эрудицию Ферма и посвятил ему свою книгу, осыпав похвалами: «Страницы этой тетради, которые остались пустыми, натолкнули меня на мысль наполнить их результатами, которые недавно сообщил мне несравненный господин Ферма, в высшей степени любезно отнесшийся ко мне во время нашей беседы». В этой же книге он пишет: «Все мудрецы, сведущие в литературе, оказывают нам помощь при толковании сложных пассажей, которые мы находим в книгах.

Я могу привести множество превосходных наблюдений, сделанных вами о Синезии, Фронтине, Афинее и о многих других авторах, а также те разъяснения, которые вы дали для изречений, оставшихся не понятыми Скалигером, Казобоном, Петавиусом и Сомме. Наконец, кажется, сеньор, что вы родились, чтобы править царством слов и быть высшим законодателем для всех мудрецов».

Эрудицию Ферма признавали многие из тех, кто его знал. Подлинный энциклопедист, не знавший границ между науками и языками, он интересовался всеми областями знаний. Ферма был готов выслушать любого и высказать свое мнение. Многие обращались к нему с просьбами о сотрудничестве.