Николай Кузанский - Сочинения в 2-х томах. Том 2

34. Кажется уместным сказать еще в отношении идей (species), которые не возникают и не гибнут, разве что в своих акциденциях, и суть подобия нетленного, божественного, бесконечного интеллекта, каким образом их можно понять, — а именно, что интеллект отражается в каждой идее, и не как одно лицо во многих зеркалах, а как одна бесконечная величина в разных конечных величинах, в любой из них целиком. Скажу, как я это себе представляю. Всякая идея конечна так, как треугольник конечен среди плоскостных величин: он первая такая конечная и определенная величина, в ней целиком отражается (resplendet) бесконечный угол. В самом деле, это максимальный и вместе минимальный, а потому бесконечный и неизмеримый угол, поскольку он не допускает ни увеличения, ни уменьшения, и он начало всех треугольников: нельзя сказать, что два прямых угла больше или меньше максимального и вместе минимального угла, ведь пока максимальный угол оказывается меньше [или больше] двух прямых, он еще не максимальный просто. Но всякий треугольник имеет три угла, равные двум прямым. Следовательно, в каждом треугольнике целиком отражается это бесконечное начало всех углов [173] Т. е. сумма углов в любом треугольнике неизменна так же, как вид (идея) в индивидах. . И еще. В том смысле, что треугольнику не предшествует никакая ограниченная прямыми линиями угловатая поверхность с одним или двумя углами, но именно треугольник — первая такая ограниченная поверхность, он тоже подобен идее и неразрушимой первосущности: треугольник не разлагается на нетреугольники, а тем самым и ни на какую фигуру, чьи три угла были бы [в сумме] больше или меньше, [чем у него]. Опять-таки треугольники могут быть разные: остроугольные, тупоугольные, прямоугольные, и в каждом снова различия. Так и идеи. И все идеи — совершенные и определенные первосущности, поскольку в них конечным и определенным образом целиком отражается первое начало со всей своей неразрушимостью и [бесконечной] величиной.

Чтобы составить себе яснее представление об этом, рассмотри через берилл максимальный и вместе минимальный треугольник, причем предметом (obiectum) окажется начало треугольников, — скажем, так, как ты видел выше в нашем символе относительно угла [174] О начале угла 8, 9. .Пусть из середины прямой аb исходит подвижная линия cd, при любом положении которой точка d соединяется с точками а и b прямыми: линиями, замыкающими соответствующие поверхности. Сколько ни изменять их, вращая линию cd вокруг точки с, ни один из двух образующихся здесь треугольников явно не станет максимальным, пока у другого еще есть какая-то величина. Если один треугольник станет максимальным, другой поэтому обязательно должен стать минимальным, что явно невозможно, пока cd не ляжет на cb и dc не окажется с b а одной прямой линией. Здесь начало углов и треугольников.

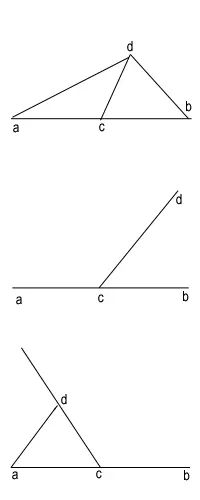
В этом начале, которое я вижу через максимальный и вместе минимальный угол и через минимальный и вместе максимальный треугольник, я вижу свернутыми все углы и вместе треугольники, так что любой угол, единый и тройственный, есть в нем само это начало. Тем самым триединое начало, вместе единое и тройственное, в любом конечном треугольнике, едином и вместе тройственном, отражается наилучшим образом, каким бесконечный [треугольник], единый и вместе тройственный, может отразиться в конечном. И еще ты видишь тут, что идея образуется через полное свертывание: когда она полностью обращается сама на себя, вполне соединяя конец с началом, как линия аb сначала складывается по точке с в угол, а потом c b складывается по точке d таким образом, чтобы b возвратилось в а. Через такое двойное обращение на себя возникает треугольник, или первая определенная нетленная идея, с совпадающими началом и концом.

35. Заметь, что и во всех других смыслах этот наш символ ясно подводит к пониманию идей. Треугольник, который мал или велик по своему видимому количеству, то есть поверхности, равен всякому другому треугольнику по числу углов и по совокупной величине этих трех углов. Таким же образом всякая идея равна всякой другой идее по своей величине, которая никак не может быть количеством, допускающим увеличение и уменьшение, но есть простая субстанциальная величина [175] Величина (magnitudo) — здесь (как ниже 46 и Охота за мудр. 34, 101-103) «величинность», начало величины до количественных определений. Ср. Тьерри Шартрский (Коммент, на Боэция «О Троице» IV 27): «Будучи великим, Бог не столько велик, сколько сама величина» . , предшествующая всякому вещественному количеству. Дальше. Видеть треугольник на плоскости — это видеть идею в субстрате, идеей которого она является. И я вижу в нем возникающую субстанцию, которая есть его «бытие тем, что было»; скажем, данный треугольник прямоугольный потому, что он есть «бытие тем, что было» прямоугольного треугольника. Все это достигается через идею. Она [кроме того] дает ему быть таким-то; заметь: она дает [треугольнику] не только быть треугольником вообще, но быть именно или треугольным, или остроугольным, или тупоугольным, или каким-то еще подробнее различенным треугольником внутри каждого из этих видов. Таким же образом идея (species) есть спецификация рода через [видовое] различие; спецификация есть связь, связывающая это различие с родом. Итак, идея дает вещи все ее бытие. Причем, оказываясь всякий раз иной, идея вовсе не изменяется под действием субстрата, но в самой себе имеет свои сущностные начала, через которые определяется как субстанция. Так фигура заключена в своей определенности. Это подобно тому, что мы видим в гармонии, или числовых соразмерностях. Гармонические идеи разнообразны; в них через разнообразные различия разнообразно специфицируется всеобщая гармония. Связь, связующая разное — скажем, высокое с низким, — а это и есть идея, хранит в себе соразмерную гармоничность, определявшуюся через свои сущностные начала отлично от всякой другой идеи. Идея есть как бы некое гармоническое соотношение, которое, хоть оно и одно, может сообщаться многим субстратам. Такое соотношение, или соразмерность, неразрушимо и может быть названо идеей, поскольку не допускает ни увеличения, ни уменьшения. Оно дает субстрату идею, или красоту, подобно тому как соразмерность украшает прекрасные [вещи]. А в гармонической, или согласной, соразмерности светится подобие вечного разума, или интеллекта божественного создателя, и мы на опыте знаем это потому, что пропорция сладостна и приятна всякому чувству, пока оно ее ощущает.

36. Вот как точен символ, взятый из области чисел, если понимать числа в качестве соразмерности, или соотношения. Это соотношение становится в числах осязаемым, как треугольник становится осязаемым на плоскости, то есть в количестве. И насколько дискретное количество проще непрерывного количества, настолько идею лучше видеть в символе дискретного количества, чем непрерывного. В самом деле, математика имеет дело с умопостигаемой матерней, как хорошо сказал Аристотель [176] Мет. VII 10, 1036a 4-12; 11, 1037a 4. . Но эта ее материя — величина, без которой математик не может ничего представить, и дискретная величина проще, чем непрерывная, она более духовна и тем самым более подобна совершенной простоте идеи; хотя, конечно, простота идеи, то есть чтойности, опережает простоту дискретной величины. Поскольку она опережает вообще всякую величину, какую можно помыслить, ее помыслить нельзя: никакое интеллектуальное понятие не может возникнуть помимо величины и в лучшем случае доходит только до вышеупомянутой дискретной величины, отвлеченной от чувственного дискретного количества. Тем самым первую субстанцию, чья простота предшествует всем способам существования ее акциденций, будь то в чувственном бытии или в математическом, отвлеченном от чувственности, наш интеллект не может представить, будучи привязан к телу, то есть количеству, как к инструменту своих представлений. Однако он видит, что она — над всяким его представлением. Рассмотри еще вот что. Один цвет нам приятнее другого, и то же голос, или пение, и прочие чувственные вещи, потому что ощущение есть жизнь чувствующей души, причем не то или иное ощущение, а ощущение всего ощущаемого сразу, и значит, прежде всего такое ощущение, при котором она воспринимает больше от своего объекта, а именно, когда ощущаемое пребывает в каком-то гармоническом единстве, — скажем, когда какой-либо цвет гармонически содержит в себе многие цвета, гармоническое пение соединяет много различных тонов и так далее в отношении прочих ощущений. То же самое в умопостигаемых вещах, когда в одном начале [душа улавливает] много умопостигаемого разнообразия. Из-за этого понимание первого начала, в котором все основание вещей, есть высшая жизнь интеллекта и его бессмертное наслаждение. Так же и идея (species) есть некая целостность одного из совершенных модусов уподобления божественному бытию, свертывающая в себе все частные определения и конкретизующаяся в субстрате до этого вот бытия. Не раз уже описанным способом ты сможешь через наш берилл видеть и это [первое] начало, и то, как божественны все идеи благодаря своей субстанциальной, совершенной уподобленности вечному разуму, и то, что в них обнаруживает себя творящий интеллект, и то, что всякая идея есть слово или намерение этого интеллекта, являющего себя в данной идеальной определенности (specifice). Такая идея — подлинная суть всякого индивида, недаром всякий индивид благоговейно чтит эту свою идею и всячески заботится, чтобы не потерять ее; хранить ее — для него высшее наслаждение и исполнение всех желаний.