Георгий Рузавин - Методология научного познания [Учебное пособие для вузов]

Е — истинно,

Н — вероятно

где Н. — гипотеза или обобщение; Е — свидетельство, подтверждающее его; р(Н/Е) — вероятность гипотезы Н на основе свидетельства Е.

Следует обратить особое внимание на то, что подтверждение следствия гипотезы имеет не окончательный, а относительный характер, так как не исключается возможность обнаружения другого свидетельства или факта, который может опровергнуть гипотезу. Именно поэтому рассматриваемая схема не является логическим законом или правилом вывода. В отличие от нее опровержение гипотезы на основе ложного следствия действительно представляет логическое правило вывода, которое в логике известно как modus tollens.

2. Правило логического опровержения гипотез имеет следующий вид:

Если из Н следует Е или [ (H Е) & Е ] H

Е — ложно

H — ложно

С логической точки зрения опровержение гипотезы имеет окончательный характер, поэтому ложная гипотеза отбрасывается.

С помощью дедукции следствий из гипотез и других общих утверждений науки (обобщений, законов и теорий) делаются, как известно, прогнозы и предсказания, которые являются наиболее убедительными свидетельствами правдоподобности их истинности. В таких науках, как астрономия, физика или химия, такие предсказания отличаются особой точностью. Например, в астрономии предсказания солнечных и лунных затмений рассчитываются на десятки и сотни лет вперед, а физика с помощью своих теорий предсказала существование не только молекул и атомов, но и элементарных частиц материи. Однако в отличие от обобщений универсального характера, которые применяются в наиболее развитых отраслях естествознания, в социально-экономических и гуманитарных науках ученые и исследователи опираются преимущественно на статистические обобщения, заключения которых только вероятны.

Исследование и проверка гипотез не служат конечной целью науки. Они представляют собой лишь путь к открытию законов науки, поскольку именно гипотезы наиболее общего характера, тщательно подтвержденные, обоснованные и проверенные, становятся законами. Но законы науки также не являются абсолютными истинами, а только относительными.

В законах науки отображаются регулярные, повторяющиеся связи или отношения между явлениями или процессами реального мира. Начиная с древних греков и вплоть до конца XIX в. подлинными законами науки считались универсальные утверждения, раскрывающие регулярно повторяющиеся, необходимые и существенные связи между явлениями. Между тем регулярность может иметь и не универсальный, а экзистенциальный характер, т. е. относиться не ко всему классу, а только к определенной ее части. Поэтому с точки зрения области действия все законы можно разделить на два основных вида, которые охарактеризованы ниже.

Универсальные и частные законы. Универсальными принято называть законы, которые отображают всеобщий, необходимый, строго повторяющийся и устойчивый характер регулярной связи между явлениями и процессами объективного мира. Иначе говоря, термин «регулярность» используется здесь в смысле неизменной повторяемости, характерной для существенной связи явлений.

В качестве примера рассмотрим хорошо известный закон теплового расширения тел, который на качественном языке может быть выражен с помощью предложения: «Все тела при нагревании расширяются». Более точно он выражается на количественном языке посредством функционального отношения между температурой и увеличением размеров тела. На языке современной логики этот и другие универсальные законы могут быть представлены в форме общей импликации: (х) [P(х) Q(x) ], которая читается так: «Для всякого x, если x обладает свойством Р, то оно обладает также свойством Q», где (х) обозначает универсальный квантор, указывающий, что данная импликация применима ко всем х. В нашем примере x обозначает любое физическое тело, а импликацию можно представить в виде условного высказывания: «Если тело нагреть, то оно расширится».

Частные , или экзистенциальные, законы представляют собой либо законы, выведенные из универсальных, либо законы, отображающие регулярности случайных массовых событий, о которых речь пойдет ниже. К числу частных можно отнести, например, закон теплового расширения металлов, который является вторичным, или производным, по отношению к универсальному закону теплового расширения всех физических тел.

Логическая форма представления таких законов отличается от универсальных тем, что перед импликацией стоит экзистенциальный квантор, или квантор существования, который указывает, что стоящая за ним импликация относится не ко всему классу, а лишь к подклассу тел:

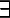х[Р{х) (х)],

где 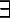х — квантор существования, означающий что указанным свойством обладают лишь некоторые х.

Детерминистические и стохастические законы. По точности предсказаний различают законы детерминистические и стохастические. Предсказания, основанные на детерминистических законах, имеют вполне достоверный, точный характер. В отличие от них стохастические, или вероятностно-статистические , законы дают лишь вероятностные предсказания. Такие законы отображают определенную регулярность, которая возникает в результате взаимодействия случайных массовых или повторяющихся событий. Простейшим примером может служить бросание игральной кости, представляющей собой правильный кубик, на гранях которого нанесены очки от 1 до 6. При отдельном бросании мы не можем определить, какая при этом выпадет грань. Но если повторить количество подбрасываний много раз, то можно убедиться, что каждая грань появится с относительной частотой, равной 1/6. На этом основании вероятность подобного случайного массового или повторяющегося события можно определить как относительную частоту появления такого события при достаточном числе испытаний:

Р = m/n,

где Р — вероятность; m — число появления события; n — число всех испытаний.

Более точно вероятность теоретически можно было бы определить как предел относительной частоты события при неограниченном числе испытаний. Но такое число испытаний осуществить невозможно, поэтому практически ограничиваются достаточным числом, определяемым условиями конкретной задачи.