Валентин Асмус - ЛОГИКА

Таким образом, закон противоречия и сам по себе и в соединении с законом исключённого третьего действительно обусловливает в умозаключении логическую связь между посылками и заключением. Но связь эта опирается также и на закон тождества . Заключение, выведенное из посылок, не могло бы быть истинным, если бы термины «бамбуки», «злаки», «цветущие колосками», появляющиеся в умозаключении каждый дважды, мыслились не в тождественном смысле, т. е. если бы в умозаключении был бы где-нибудь нарушен закон тождества. Если бы, например, под «злаками» в одной из посылок мыслилось одно содержание, а в другой — иное, то заключение об отношении между «злаками» и «цветущими колосками» из таких посылок не могло бы быть выведено. Заключение это возможно только на основе раскрытого в посылках отношения каждого из этих понятий к понятию «злаки». Но совершенно очевидно, что если понятие «злаки» в обеих посылках не тождественно, то невозможно установить посредством этого понятия никакой логической связи между понятием «бамбуки» и понятием «цветущие колосками».

Таким образом, все четыре логических закона мышления — закон тождества, закон противоречия, закон исключённого третьего и закон достаточного основания — применяются во всех умозаключениях. Без этих законов в умозаключениях не могла бы быть усмотрена логическая связь между посылками и заключением.

Всякое правильное умозаключение раскрывает для нашей мысли необходимое отношение между предметами, которые мыслятся в посылках и в выводе. Так, посылка «все злаки цветут колосками» выражает мысль о том, что свойство цветения колосками есть необходимое свойство всех злаков; поэтому все предметы, называемые злаками, необходимо входят в число «цветущих колосками» (см. рис. 34).

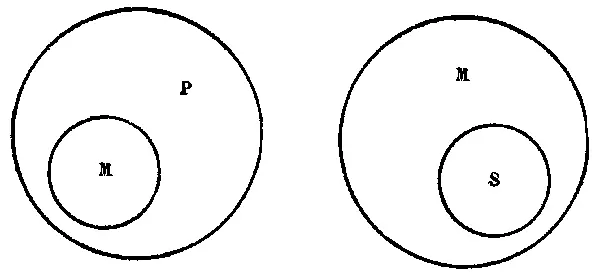
Рис. 34. . . . . . . . . . . . . . . . . . . . . . . . Рис. 35

На этом рисунке объём понятия «злаки» изображён посредством круга М, объём понятия «цветущие колосками» — посредством круга Р. Из рисунка видно, что все злаки необходимо принадлежат к цветущим колосками, т. е. что все М необходимо принадлежат к Р. Посылка «все бамбуки — злаки» выражает мысль о том, что свойства злаков необходимо являются свойствами бамбуков; поэтому все предметы, называемые «бамбуками», необходимо входят в число злаков (см. рис. 35).

На этом рисунке объём понятия «бамбуки» изображён посредством круга S, объём понятия «злаки» — посредством круга М. Из рисунка видно, что все бамбуки необходимо принадлежат к злакам, т. е. что все S необходимо принадлежат к М. Сопоставляя обе эти посылки, получаем вывод: «все бамбуки цветут колосками». Вывод этот выражает мысль о том, что свойство всех злаков цвести колосками необходимо является также свойством всех бамбуков; поэтому все предметы, называемые «бамбуками», необходимо входят в число «цветущих колосками» (см. рис. 36).

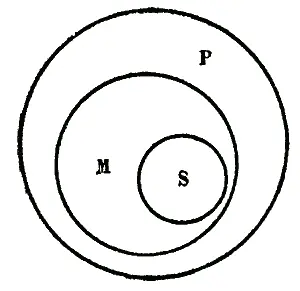
Рис. 36

Из этого рисунка ясно, что не только все злаки необходимо цветут колосками, как это было видно из первой посылки, и что не только все бамбуки — необходимо злаки, как это было видно из второй посылки, но что, кроме того, все бамбуки необходимо цветут колосками. Необходимость вывода непреложно следует из истинности посылок: так как, согласно уже разъяснённым отношениям между свойствами бамбуков, злаков и цветущих колосками, весь объём понятия «злаки» (круг М) входит в объём понятия «цветущие колосками» (круг Р) и так как весь объём понятия «бамбуки» (круг S) входит в объём понятия «злаки» (тот же круг М), то весь объём понятия «бамбуки» необходимо должен входить в объём понятия «цветущие колосками» (весь круг S необходимо должен быть внутри круга Р).

Если бы кто, признавая, что «все бамбуки — злаки» и что «все злаки цветут колосками», стал бы в то же время отрицать, что «все бамбуки цветут колосками», то это было бы равносильно тому, как если бы кто, признав, что круг М помещается весь внутри круга Р и что круг S помещается весь внутри круга М, стал бы в то же время отрицать то, что круг S весь помещается внутри круга Р. Человек, мыслящий таким образом, оказался бы в противоречии с собственной мыслью: соглашаясь с посылками, он мыслил бы круг S целиком внутри круга Р (см. рис. 36а); в это же время, отрицая вывод, он мыслил бы круг S вне круга Р (см. рис. 37).

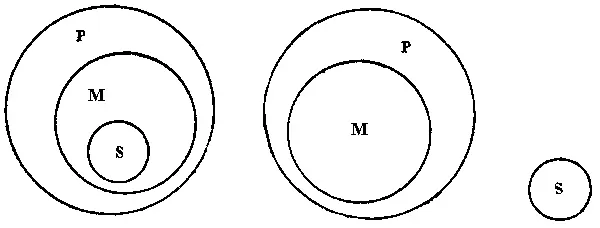
Рис. 36а. . . . . . . . . . . . . . . . . Рис. 37

§ 6. Так как умозаключение 1) даёт в выводе мысль новую сравнительно с мыслями, выраженными в посылках, и 2) раскрывает необходимость связи между посылками и выводом, то умозаключение есть очень важная форма логического мышления. Там, где мы сразу непосредственно не видим связи между двумя понятиями, мы можем найти эту связь посредством третьего понятия, если нам только известно, в каком отношении это третье понятие стоит к каждому из наших двух понятий, связь между которыми мы стремимся выяснить. Именно эту задачу и решает умозаключение. Два понятия, отношение между которыми не видно непосредственно, умозаключение связывает посредством третьего понятия, зная отношение этого третьего понятия к каждому из них в отдельности.

Особенно важно, что связь между понятиями, раскрываемая умозаключением, есть связь необходимая. Если посылки истинны и если в ходе умозаключения мы не сделали никакой логической ошибки, то вывод всегда будет необходимо истинным. Умозаключение раскрывает не такую связь между посылками и выводом, которая может быть истинной, но может и не быть истинной. Умозаключение раскрывает необходимость связи, существующей между посылками и выводом. Кто убедился в истинности посылок, тот должен согласиться, тот не может не согласиться с истинностью вывода.

Это свойство умозаключений — логическая необходимость всякого правильного вывода, полученного из истинных посылок, — делает умозаключение важным звеном в доказательстве и в опровержении , во всякого рода спорах и дискуссиях . Умозаключение — могучее средство убеждения. Так, получив в беседе или в споре согласие противника с посылками, мы легко можем заставить его согласиться и с выводом, как только мы покажем, что принятые им посылки необходимо вынуждают к согласию также и с выводом. Рассматривая ранее доказанные теоремы как посылки умозаключения, мы можем показать, что новая теорема, которую мы взялись доказать, есть не что иное, как вывод, необходимо вытекающий из истинности этих посылок, и т. д.