Валентин Асмус - ЛОГИКА
- Название:ЛОГИКА
- Автор:
- Жанр:
- Издательство:ОГИЗ
- Год:1947
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Валентин Асмус - ЛОГИКА краткое содержание
Предлагаемая книга представляет систематическое изложение учений логики. Она может быть использована студентами высших учебных заведений, аспирантами научно-исследовательских институтов и лицами, приступающими к самостоятельному изучению логики. Преподаватели логики в средней школе найдут в ней подробное освещение вопросов, входящих в программу их предмета, но лишь кратко излагаемых в учебниках логики для старшего класса.
ЛОГИКА - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Силлогизмы могут иметь различное строение посылок, и потому самые выводы в них могут стоять в зависимости от различных правил. Логика устанавливает все эти правила и изучает все разновидности силлогизмов.
§ 10.Первая группа силлогизмов — так называемые простые категорические силлогизмы. Так называются силлогизмы, в которых вывод получается из двух посылок и в которых обе посылки суть суждения категорические.
Рассматривая встречающиеся в практике мышления простые категорические силлогизмы, можно заметить, что расположение понятий, или терминов, в посылках этих силлогизмов может быть различным.
Рассмотрим следующий силлогизм:
| Все амфибии — позвоночные. | М—Р | |||
| Все лягушки — амфибии. | S—M | |||
| ——————————— | ——— | |||
| Все лягушки — позвоночные. | S—P |
В нём средний термин в большей посылке является субъектом, а в меньшей — предикатом.
Силлогизм, в котором понятия, или термины, расположены таким образом, называется силлогизмом первой фигуры .
В нашем примере силлогизма первой фигуры меньшая посылка («все лягушки — амфибии») выясняет, что весь объём класса S входит как часть в более обширный объём класса М (см. рис. 38).
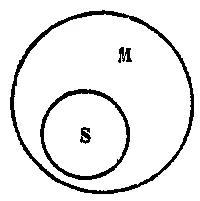
Рис. 38
Бо́льшая посылка («все амфибии — позвоночные») выясняет, что этот более обширный объём класса М весь входит как часть в ещё более обширный объём класса Р (см. рис. 39).
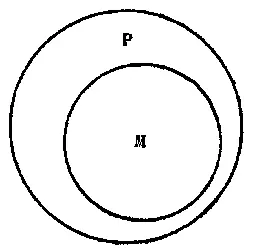
Рис. 39
Сопоставляя эти отношения понятий, выяснившиеся из посылок, устанавливаем в выводе («все лягушки — позвоночные») принадлежность класса S, имеющего наименьший объём, к классу Р, имеющему наибольший объём (см. рис. 40).
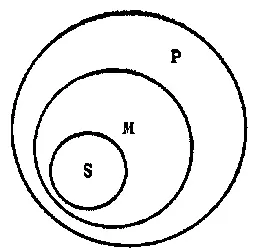
Рис. 40
§ 11.Рассмотрим теперь другой пример силлогизма:
Все звёзды светят собственным светом.
Ни одна планета не светит собственным светом.
—————————————————
Ни одна планета, не есть звезда.
Вывод этот — силлогизм. В нём заключение, или вывод («ни одна планета не есть звезда»), получено из двух посылок. В посылках этих устанавливается отношение субъекта вывода («планета») и предиката вывода («звезда») к третьему, или среднему, понятию («тело, светящее собственным светом»). Именно через отношение среднего понятия к понятиям «планета» и «звезда» выясняется отношение этих последних между собой.
И действительно: бо́льшая посылка («все звёзды светят собственным светом») устанавливает, что весь объём класса Р входит в объём класса М (см. рис. 41).
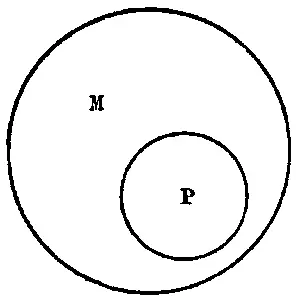
Рис. 41
Меньшая посылка («ни одна планета не светит собственным светом»)устанавливает, что класс не принадлежит к классу М, т. е. что весь объём класса S целиком находится вне объёма класса М (см. рис. 42).
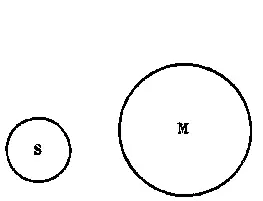
Рис. 42
Сопоставляя эти отношения понятий, выяснившиеся из посылок, заключаем в выводе («ни одна планета не есть звезда»), что класс S не принадлежит к классу Р, т. е. что весь объём класса S находится вне всего объёма класса Р (см. рис. 43).
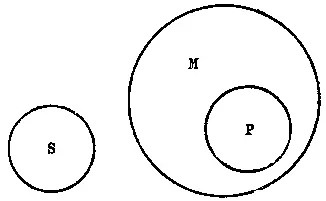
Рис. 43
Присматриваясь к расположению терминов в посылках и в выводе этого силлогизма, замечаем, что это расположение
Р — М
S — M
———
S — Р
отличается от расположения терминов в силлогизме первой фигуры:
М — Р
S — M
———
S — Р
А именно: во втором силлогизме средний термин в обеих посылках — большей и меньшей — является предикатом . Силлогизм с таким расположением терминов называется силлогизмом второй фигуры.
§ 12.Рассмотрим третий пример силлогизма:
Все утконосы — животные, кладущие яйца.
Все утконосы — млекопитающие.
————————————————————
Некоторые млекопитающие — животные, кладущие яйца.
И этот вывод —силлогизм. И в нём на основе устанавливаемого в двух посылках отношения понятия «млекопитающие» и понятия «животные, кладущие яйца» к третьему понятию («утконосы») устанавливается отношение субъекта к предикату в заключении.
Бо́льшая посылка («все утконосы — животные, кладущие яйца») устанавливает, что класс М принадлежит к классу Р, т.е. что весь объём класса М входит как часть в объём класса Р (см. рис. 44).
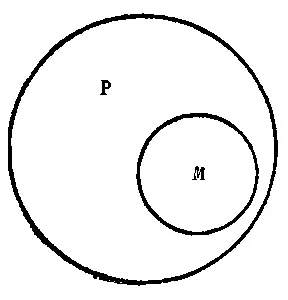
Рис. 44
Меньшая посылка («все утконосы — млекопитающие») устанавливает, что класс М принадлежит к классу S, т. е., что весь объём класса М входит как часть в объём класса S (см. рис. 45).
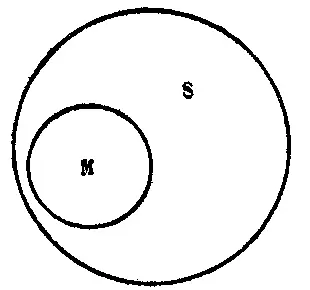
Рис. 45
Сопоставляя эти отношения понятий, выяснившиеся из посылок, заключаем в выводе («некоторые млекопитающие — животные, кладущие яйца»), что какая-то часть класса S принадлежит к классу Р, т. е. объём S в какой-то своей части совпадает с объёмом Р (см. рис. 46).
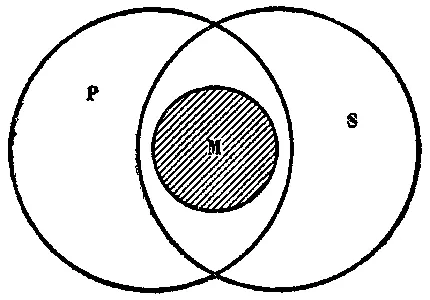
Рис. 46
И действительно, так как весь объём М целиком помещается как внутри объёма S, так и внутри объёма Р, то все те части объёма S, которые заняты объёмом М, будут в то же время и частями объёма Р. И наоборот: все те части объёма Р, которые заняты объёмом М, будут в то же время и частями объёма S.
Рассмотрим расположение терминов в последнем силлогизме:
М — Р
М — S (III)
———
S — P
Здесь расположение терминов отличается от их расположения в силлогизмах первой и второй фигуры:
| M — P | P — M | |||||||
| S — M | (I) | и | S — M | (II) | ||||
| ———— | ———— | |||||||
| S — P | S — P |
А именно: в третьем силлогизме средний термин в обеих посылках оказывается субъектом . Силлогизм с таким расположением терминов называется силлогизмом третьей фигуры.
Читать дальшеИнтервал:
Закладка:









