Валентин Асмус - ЛОГИКА

Так как средний термин в обеих посылках не распределён, то в каждой посылке имеется в виду какая-то неопределённая точно часть его объёма. При таком положении вполне возможно, что в одной посылке речь идёт о какой-то одной, а в другой посылке — о какой-то другой части объёма среднего термина (см. рис. 48).

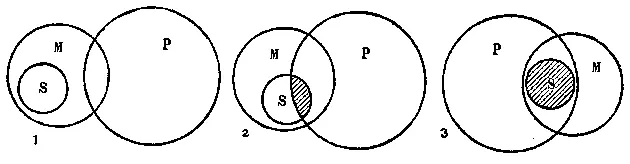
Рис. 48

На рисунке изображены отношения понятий, выражаемые посылками. Объём понятия «млекопитающие» изображён кругом М, объём понятия «тюлени» — кругом S, объём понятия «водные животные» — кругом Р. Из рисунка видно, что посылки оставляют нас в неизвестности об отношении между понятиями S и Р. Так как из посылок неизвестно, какую именно часть объёма М составляет объём S и какую именно часть объёма Р составляет объём М, то остаются открытыми три возможности: 1) весь объём S находится вне всего объёма Р; 2) объёмы S и Р совпадают частично ; 3) объём S целиком входит как часть в объём Р. Но это значит, что связь между субъектом и предикатом вывода, которая должна была бы быть раскрыта через их отношение к среднему термину, не может быть установлена: в сущности здесь даже нет среднего термина, а есть два означаемые одним словом понятия, из которых одно, возможно, отмечает одну часть объёма, а другое — другую.

§ 18.Четвёртое общее правило формулируется так: если больший или меньший термины не распределены в посылках, они не могут оказаться распределёнными в выводе. Так, из посылок «все великие поэты обладают сильным воображением», «все великие поэты — впечатлительные люди» нельзя вывести, будто «все впечатлительные люди обладают сильным воображением». Здесь правильным будет только частный вывод: «некоторые впечатлительные люди обладают сильным воображением». И действительно, понятие «впечатлительные люди» — меньший термин нашего силлогизма — не распределено в посылке. В суждении «все великие поэты — впечатлительные люди» понятие «впечатлительные люди» мыслится не во всём своём объёме. Совершенно очевидно, что и в выводе, где понятие «впечатлительные люди» становится субъектом, нет достаточного основания брать это понятие во всём его объёме (см. рис. 49).

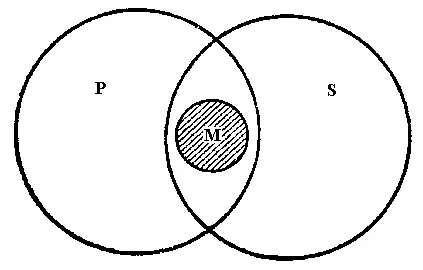
Рис. 49

На рисунке представлены отношения понятий, выражаемые посылками. Объём понятия «великие поэты» представлен кругом М, объём понятия «люди, обладающие сильным воображением»» — кругом Р, объём понятия «впечатлительные люди» — кругом S. Из посылок видно, что в объём Р безусловно входит вся та часть объёма S, которая занята объёмом М. Поэтому посылки дают правильный вывод: « некоторые S принадлежат к объёму Р». Но выводить из посылок больше этого мы не вправе. Только о той части объёма S, которая совпадает с М, достоверно известно из посылок, что она входит в объём Р. А так как эта часть, равная М, не исчерпывает ни всего объёма S, ни всего объёма Р, то отсюда видно, что не все S, но лишь некоторые S принадлежат к объёму Р.

Другой пример: из посылок «все студенты должны держать экзамены» и «аспиранты — не студенты» нельзя сделать вывод, будто «аспиранты не должны держать экзаменов». В самом деле, в выводе «аспиранты не должны держать экзаменов» больший термин как предикат отрицательного суждения был бы распределён. Но в большей посылке — «все студенты должны держать экзамены» — больший термин как предикат утвердительного суждения (ср. гл. VI, § 25) не распределён. Понятно, что, не будучи распределён в посылке, он не может оказаться распределёнными в выводе (см. рис. 50).

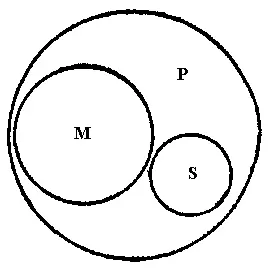
Рис. 50

На рисунке представлены отношения понятий, выражаемые посылками. Объём понятия «студенты» представлен кругом М, объём понятия «лица, обязанные держать экзамены» — кругом Р и объём понятия «аспиранты» — кругом S. Из рисунка видно, что мы не вправе заключать, будто объём S необходимо будет находиться вне объёма Р. Так как термин Р не распределён, то объём М составляет лишь какую-то часть объёма Р. Поэтому вполне возможно, что весь объём S, о котором из другой посылки нам известно, что он не входит в объём М, окажется всё же целиком внутри объёма Р — как другая, наряду с М, часть этого объёма (1). В нашем примере так оно и есть: аспиранты, не будучи студентами, всё же принадлежат к числу лиц, обязанных держать экзамены.

§ 19.Пятое общее правило формулируется так: если обе посылки отрицательны, то из них нельзя получить никакого вывода. Так, из посылок «киты — не рыбы» и «дельфины — не рыбы» нельзя сделать никакого вывода об отношении дельфинов к китам. И действительно, обе посылки здесь — отрицательные. Из них видно, что весь объём большего и весь объём меньшего термина вне всего объёма среднего термина: ни один кит и ни один дельфин не входят в число рыб. Но зная это, мы ещё ничего не знаем о том, в каком отношении друг к другу находятся объёмы большего и меньшего терминов: они могут стоять вне друг друга, могут частично совпадать и могут оказаться один внутри другого (см. рис. 51).

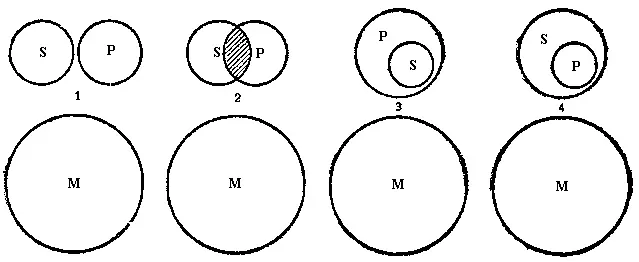
Рис. 51

На рисунке представлены отношения понятий, выражаемые посылками. Объём понятия «рыбы» представлен кругом М, объём понятия «дельфины» — кругом S, объём понятия «киты»— кругом Р. Из рисунка видно, что мы не вправе сделать какое бы то ни было заключение о необходимом отношении объёма S к объёму Р. Из того, что весь объём S находится вне объёма М и весь объём Р также находится вне объёма М, ещё не видно, в каком отношении будет объём S к объёму Р. Рисунок показывает, что здесь остаются открытыми четыре возможности: весь объём S находится вне всего объёма Р; 2) объёмы S и Р частично совпадают между собой; 3) объём S целиком входит как часть в объём Р; 4) объём Р целиком входит как часть в объём S.

§ 20.Шестое общее правило формулируется так: если вывод из данных посылок вообще возможен и если одна из посылок при этом отрицательная, то вывод также будет отрицательный.

Рассмотрим силлогизм:

Ни один злак не есть споровое растение.

Пшеница — злак.

———————————————

Пшеница не есть споровое растение.

Здесь одна из посылок — отрицательная, а другая — утвердительная. Это значит, что объём одного из терминов, входящих в вывод, стоит вне объёма среднего термина, а объём другого термина, входящего в вывод, составляет часть объёма среднего термина (см. рис. 52).