Валентин Асмус - ЛОГИКА
- Название:ЛОГИКА
- Автор:
- Жанр:
- Издательство:ОГИЗ
- Год:1947
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Валентин Асмус - ЛОГИКА краткое содержание
Предлагаемая книга представляет систематическое изложение учений логики. Она может быть использована студентами высших учебных заведений, аспирантами научно-исследовательских институтов и лицами, приступающими к самостоятельному изучению логики. Преподаватели логики в средней школе найдут в ней подробное освещение вопросов, входящих в программу их предмета, но лишь кратко излагаемых в учебниках логики для старшего класса.
ЛОГИКА - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Различия между тремя фигурами простого категорического силлогизма представляют интерес не только потому, что термины в посылках этих силлогизмов размещены различным образом. Различное расположение терминов в посылках связано с различным отношением между содержанием и объёмом понятий, входящих в посылки и в выводы. И действительно: от того, будет ли, например, средний термин субъектом посылки или её предикатом, зависит распределённость среднего термина в посылках, т. е. возможность мыслить средний термин во всём объёме или только в части его объёма. То же справедливо и относительно большего и меньшего термина. В свою очередь от отношения между содержанием и объёмом понятий, входящих в посылки и в выводы, зависит различная ценность фигур силлогизма для логического мышления и знания, а потому различная роль, какую каждая из фигур играет в доказательствах и рассуждениях.
§ 13.Чтобы выяснить роль каждой фигуры, т. е. характер выводов, которые могут быть получены посредством этой фигуры, необходимо познакомиться с разновидностями фигур, или модусами .
Сравнивая различные выводы, сделанные по одной и той же фигуре, замечаем, что силлогизмы одной и той же фигуры могут различаться между собой качеством и количеством посылок и вывода.
Сравним два силлогизма:
| Все злаки — однодольные растения. | Ни один злак не есть двудольное растение. | |
| Все бамбуковые — злаки. | Все бамбуковые — злаки. | |
| ———————————— | ———————————— | |
| Все бамбуковые — однодольные растения. | Ни одно бамбуковое не есть двудольное растение. |
Оба эти силлогизма — силлогизмы первой фигуры, так как в обоих средний термин является субъектом в большей и предикатом в меньшей посылке. Но в то же время между этими двумя силлогизмами первой фигуры имеется и различие. Состоит оно в различном качестве посылок и вывода. В первом силлогизме обе посылки и вывод — суждения общеутвердительные. Схема этого силлогизма:
А
А
—
А
Во втором силлогизме бо́льшая посылка есть суждение общеотрицательное, меньшая — общеутвердительное, вывод — суждение общеотрицательное. Схема этого силлогизма:
Е
А
—
Е
Сравним ещё два силлогизма:
| Все грибы — споровые растения. | Ни одна планета не есть звезда. | |
| Некоторые бесцветковые — грибы. | Некоторые светила — планеты. | |
| ———————————— | ———————————— | |
| Некоторые бесцветковые — споровые растения. | Некоторые светила — не звёзды. |
Оба эти силлогизма — также силлогизмы первой фигуры, так как в обоих средний термин является субъектом в большей и предикатом в меньшей посылке. Но в то же время между этими двумя силлогизмами первой фигуры имеется и различие. Состоит оно в различном качестве и количестве посылок и вывода. В первом силлогизме и посылки и вывод по качеству — суждения утвердительные. По количеству же большая посылка — суждение общее, меньшая — частное, вывод — также частное. Схема этого силлогизма:
А
I
—
I
Во втором силлогизме бо́льшая посылка есть суждение общеотрицательное, меньшая — частноутвердительное, вывод — суждение частноотрицательное. Схема этого силлогизма:
Е
I
—
О
Сравнивая качество и количество выводов во всех четырёх примерах силлогизма первой фигуры, приведённых выше, видим, что в первом примере вывод — общеутвердительный («все бамбуковые — однодольные растения»), во втором — общеотрицательный («ни одно бамбуковое не есть двудольное растение»), в третьем - частноутвердительный («некоторые бесцветковые — споровые растения»), в четвёртом — частноотрицательный («некоторые светила — не звёзды»).
Разновидности силлогизмов одной и той же фигуры, обусловленные различным качеством и количеством посылок и выводов, называются модусами (от латинского слова, «modus», означающего «способ», «вид»).
§ 14.Итак, среди выводов простого категорического силлогизма могут встретиться выводы всех возможных видов качества и количества: А, Е, I и О. Но мы уже знаем, что различные по качеству и по количеству суждения имеют различное применение в знании и различную ценность для знания. Поэтому при изучении силлогизмов всех трёх фигур большой интерес представляет вопрос, какие именно модусы может дать каждая фигура силлогизма, иначе говоря, какими могут быть выводы этой фигуры по качеству и по количеству.
Для ответа на этот вопрос необходимо прежде всего исследовать, все ли теоретически возможные модусы, т. е. все ли сочетания посылок, отличающиеся только качеством и количеством, способны давать правильные выводы.
Исследование показывает, что не всякий теоретически возможный модус, т. е. не всякое сочетание качества и количества в посылках силлогизма, даёт правильный вывод.
Рассмотрим, например, суждения:
Все студенты обязаны держать экзамены.
Все аспиранты — не студенты.
В этих суждениях налицо три понятия, расположенные по схеме первой фигуры простого категорического силлогизма. Термин «студенты» в одной из посылок является субъектом, в другой — предикатом. В одной посылке устанавливается отношение терминй «студенты» к одному понятию, в другой — отношение того же термина к другому понятию.
Итак, расположение терминов в суждениях как будто в точности соответствует схеме первой фигуры:
М — Р
S — M
Первое суждение будет общеутвердительное, второе — общеотрицательное.
Схематически количество и качество этих суждений будет следующее:
А
Е
Но хотя расположение терминов в этом случае как будто отвечает условиям первой фигуры, правильный вывод из этих двух посылок невозможен . Из того, что «все студенты обязаны держать экзамены», и из того, что «все аспиранты — не студенты», никак нельзя вывести в качестве необходимого заключения, что, например, «аспиранты не обязаны держать экзамены». Хотя первая посылка выясняет отношение «студентов» к «лицам, обязанным держать экзамены»; а вторая — отношение «студентов» к «аспирантам», — отношения эти не таковы, чтобы из них видно было, каким должно быть отношение «аспирантов» к «лицам, обязанным держать экзамены». Как видно из рисунка (см. рис. 47), здесь логически возможны — при данных посылках — три случая.
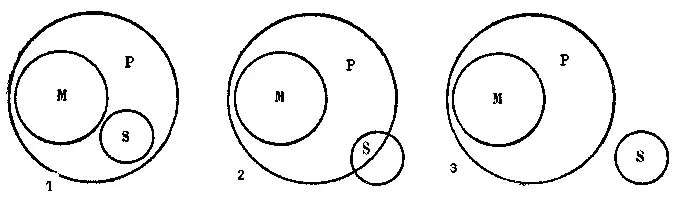
Рис. 47
Не будучи студентами (М), аспиранты (S) 1) могут все принадлежать к числу лиц, обязанных держать экзамены (Р), 2) могут принадлежать к числу этих лиц лишь в некоторой своей части и 3) могут вовсе не принадлежать к числу этих лиц.
Читать дальшеИнтервал:
Закладка:









