Карл Поппер - Открытое общество и его враги

(3) Для объяснения строения первичных тел в «Тимее» Платон обращается к понятиям элементарного квадрата и элементарного равностороннего треугольника. Эти две фигуры, в свою очередь, составлены из двух различных видов субэлементарных треугольников: полуквадрата, длина одной из сторон которого кратна √2, и половины равностороннего треугольника, длина одной из сторон которого кратна √3. Вопрос, почему Платон избрал именно эти два треугольника, а не квадрат и равносторонний треугольник, широко обсуждался. Исследователей интересовал также вопрос (см. п. (4) далее), почему он строил элементарные квадраты из четырех, а не из двух полуквадратов, а элементарный равносторонний треугольник — из шести, а не из двух субэлементарных треугольников. (См. рис. 1 и 2).

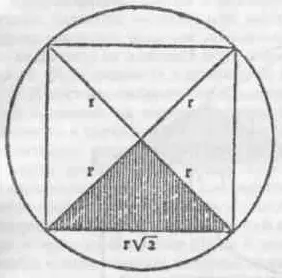
Рис. 1. Платоновский элементарный квадрат, составленный из четырех субэлементарных равнобедренных прямоугольных треугольников

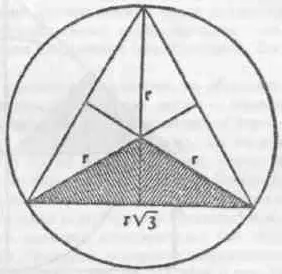
Рис. 2. Платоновский элементарный равносторонний треугольник, составленный из шести субэлементарных неравнобедренных треугольников

Как мне кажется, большинство исследователей не сумели понять того, что Платон, горячо интересуясь проблемой иррациональности, не стал бы вводить две иррациональные величины √2 и √3 (о которых он отчетливо говорит в отрывке «Тимей», 54 b) в свои субэлементарные треугольники, если бы он не стремился использовать именно эти иррациональные величины в качестве неделимых далее элементов его мира (Ф. Корнфорд — см. F. M. Cornford. Plato's cosmology, pp. 214, 231 и след. — долго обсуждает оба эти вопроса, однако предлагаемое им общее решение — «гипотеза», как он называет его (р. 234) — кажется мне неприемлемым. Если бы Платон действительно хотел получить некоторую «градацию» вроде той, о которой говорит Корнфорд — хотя у Платона нигде не упоминается о существовании чего-то меньшего, чем то, что Корнфорд называет «уровнем В», — то ему было бы достаточно разделить пополам стороны элементарных квадратов и равносторонних треугольников, построив элементы «уровня В» Корнфорда из четырех элементарных фигур, не содержащих иррациональных величин.) Однако, если Платон хотел привнести эти иррациональные величины в мир в качестве сторон субэлементарных треугольников, из которых состоят все вещи, то он, должно быть, полагал, что способен тем самым решить проблему «природы (соизмеримости и) несоизмеримости» («Законы», 820 с). Несомненно, что эту проблему было почти невозможно решить на основе той или иной разновидности атомистической космологии, поскольку иррациональные величины не могут быть выражены множеством каких-либо единиц, предназначенных для счета рациональных чисел. Однако, если сами единицы измерения будут выражены отрезками, находящимися в «иррациональных отношениях», то этого величайшего парадокса можно будет избежать: ведь такими единицами смогут быть измерены как рациональные, так и иррациональные величины, а потому существование иррациональных величин больше не будет казаться непостижимым или «иррациональным».

Платону было известно, что существуют и другие иррациональные величины, помимо √2 и √3. В «Теэтете» он говорит об открытии бесконечной последовательности иррациональных квадратных корней (в отрывке 148 b он говорит также и о том, что эти соображения могут быть применены «и для объемных тел», однако это не обязательно должно относиться к кубическим корням: возможно, здесь Платон имел в виду длину диагонали куба, кратную √3). В «Гиппии Большем» (303 b-с, см. также: Т. Heath, op. cit., p. 304) он упоминает о том, что путем сложения или применения других арифметических правил к иррациональным величинам могут быть получены другие иррациональные величины, а также рациональные числа. Платон, вероятно, имеет в виду, что, например, величина, задаваемая выражением 2 - √2 является иррациональной, а поэтому сложение этой величины с √2 будет давать, конечно, рациональное число). Очевидно, что если Платон хотел решить проблему иррациональности путем использования изобретенных им элементарных треугольников, то он должен был полагать, что все иррациональные величины (или, по крайней мере, кратные им числа) могут быть получены путем сложения и умножения (а) единиц, (b) √2 и (с) √3.

Конечно же, это было ошибочное утверждение, однако во времена Платона не могло еще существовать доказательства его ошибочности, а утверждение, что существуют только два вида атомарных иррациональных величин (а именно — длины диагоналей квадрата и куба с единичными сторонами) и что все другие иррациональные величины арифметически выводимы из (а) единиц (b) √2 и (с) √3 , могло казаться достаточно правдоподобным, если учесть относительный характер иррациональных величин. (Я имею в виду, что можно назвать иррациональной и диагональ квадрата с единичной стороной и сторону квадрата с единичной диагональю. Следует также помнить, что Евклид в книге X, определение 2, все еще характеризует все несоизмеримые квадратные корни «соизмеримостью их квадратов».) Поэтому Платон вполне мог верить в эту гипотезу, хотя у него не могло быть никаких ее доказательств. (Впервые ее опровержение было дано, по-видимому, Евклидом.) Существует одно несомненное упоминание о некоторой недоказанной гипотезе в том месте «Тимея», где Платон говорит о причинах предпочтения субэлементарных треугольников («Тимей», 53 c/d): «Все вообще треугольники восходят к двум, из которых каждый имеет по одному прямому углу и по два острых, но при этом у одного [полуквадрата] по обе стороны от прямого угла лежат равные углы величиной в одну и ту же долю прямого угла, ограниченные равными сторонами, а у другого [полуравностороннего] — неравные углы, ограниченные неравными сторонами. Здесь-то мы и полагаем начало огня и всех прочих тел, следуя в этом вероятности [или вероятной гипотезе], соединенной с необходимостью [доказательством]; те же начала, что лежат еще ближе к истоку, ведает бог, а из людей разве что тот, кто друг богу». И далее, сказав, что существует бесконечное множество неравнобедренных треугольников, из которых следует выбрать «наилучшие», и объяснив, почему наилучшими он считает половины равносторонних треугольников, Платон говорит («Тимей», 54 а-b; Корнфорд был вынужден смягчить этот отрывок, чтобы согласовать его со своей интерпретацией): «Обосновывать это было бы слишком долго (впрочем, если бы кто изобличил нас и доказал обратное, мы охотно признали бы его победителем)». Платон не объясняет, что он понимает под словом «это» — должно быть, он имеет в виду некоторое гипотетическое математическое свойство, оправдывающее при выборе одного треугольника, содержащего величину √2, выбор другого треугольника, содержащего √3. В свете изложенных мною соображений, я полагаю, что Платон говорит здесь о предполагаемой относительной рациональности остальных иррациональных чисел, т.е. о их соизмеримости с единицей, квадратным корнем из двух и квадратным корнем из трех.