Юрий Ивлев - Логика для юристов: Учебник.

Некоторые не философы открыли секрет физического бессмертия (человека).

К непосредственным умозаключениям относятся выводы, заключающиеся в превращении категорического суждения и обращении результата превращения (противопоставление предикату), а также в обращении категорического суждения и превращении результата обращения (противопоставление субъекту). Противопоставление предикату — это умозаключение, в котором субъектом заключения является термин, противоречащий предикату посылки, предикатом — субъект посылки, и заключение и посылка различны по качеству. Противопоставление субъекту — это умозаключение, в котором субъектом заключения является предикат посылки, предикатом заключения — термин, противоречащий субъекту посылки и заключение и посылка различны по качеству. Противопоставление предикату и противопоставление субъекту можно осуществлять и анализировать поэтапно (например, в случае противопоставления предикату сначала произвести превращение, а затем осуществить правильное обращение).

Общие схемы противопоставления предикату:

____... S суть Р___

... не- Р не суть S

... S не суть Р____

…не- Р суть S

Общие схемы противопоставления субъекту:

____... S суть Р___

… Р не суть не- S

... S не суть Р____

… Р суть не- S

Замечание.Нельзя делать выводы, называемые противопоставлением предикату и противопоставлением субъекту, из суждений с предикатами, являющимися, соответственно, универсальными и мнимыми именами.

Пусть дано умозаключение:

Некоторые хозрасчетные предприятия являются рентабельными.____

Некоторые нерентабельные предприятия не являются хозрасчетными.

Это умозаключение подпадает под общую схему противопоставления предикату. Чтобы проверить, правильное оно или нет, нужно произвести превращение исходного суждения:

Некоторые хозрасчетные предприятия являются рентабельными

Некоторые хозрасчетные предприятия не являются нерентабельными.

Затем правильно произвести обращение результата превращения:

Некоторые хозрасчетные предприятия не являются нерентабельными.

?

Частноотрицательное суждение не обращается. Следовательно, приведенное выше умозаключение не является правильным.

Для письменной проверки правильности непосредственных умозаключений можно использовать круговые схемы Эйлера.

Пусть дано умозаключение (противопоставление субъекту):

Некоторые материалисты (S) — метафизики (Р)

Некоторые метафизики (Р) не суть не материалисты (не- S )

В посылке этого умозаключения утверждается, что некоторые элементы объема имени S входят в объем имени Р. Поскольку слово “некоторые” употребляется в смысле “по крайней мере некоторые, а, может быть, и все”, то в общем случае следует допустить четыре возможности:

Заштрихованная поверхность соответствует тем элементам объема имени S, которые входят в объем имени Р. Прямоугольником представлен универсум рассуждения — в данном случае, например, класс философов.

Что говорится в заключении? Некоторые Р не суть не -S. Во всех ли случаях на приведенных схемах отражено, что (по крайней мере) некоторые элементы объема термина Р не включаются в объем термина не- S ? Заштрихуем на схемах горизонтальными линиями поверхности, соответствующие объему термина не- S . Для этого схемы начертим еще раз:

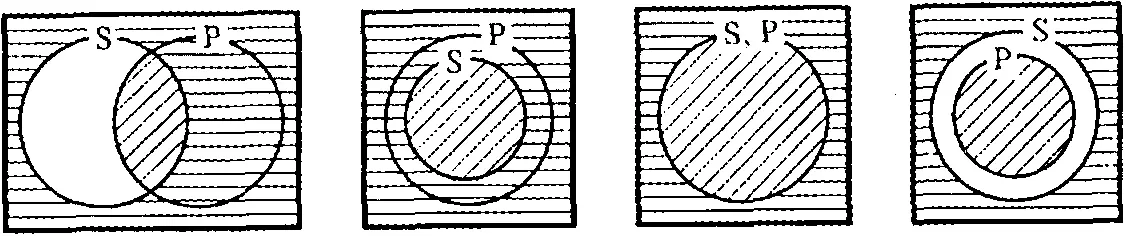
Очевидно, что во всех четырех случаях некоторые Р не являются элементами не- S . Эти элементы объема термина Р представлены поверхностями, заштрихованными наклонными линиями. Анализируемое рассуждение является правильным.

Чтобы установить, что непосредственное умозаключение не является правильным, нет необходимости рассматривать все возможные отношения между субъектом и предикатом посылки, при которых она является истинной. Достаточно найти один опровергающий случай.

Рассмотрим схему умозаключения, напоминающего обращение общеутвердительного суждения:

__Все S суть Р__

Все Р суть S

Одной из схем, представляющих возможные отношения между S и Р , при которых посылка истинна, является следующая:

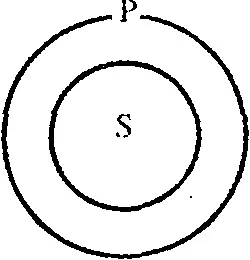
Очевидно, что в этом случае нельзя сделать вывод о том, что все Р суть S, т.е. обращение общеутвердительного суждения без ограничения невозможно (является неправильным).

Покажем, что обращение частноотрицательного суждения

Некоторые S не суть Р

Некоторые Р не суть S

не являются правильным умозаключением. Одной из схем, представляющих возможные отношения между S и Р при истинности частноотрицательного суждения, является:

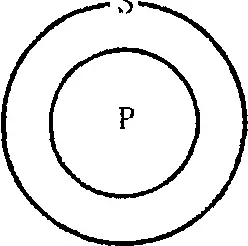
Нельзя утверждать, что некоторые Р не суть S.

Метод, который применен для исследования непосредственных умозаключений, заключается в выполнении следующих действий: первое— выявить все возможные отношения между терминами посылки, при которых она является истинной; второе— проверить, истинно ли заключение при каждом из выявленных отношений. Если да, то умозаключение правильное. Если заключение ложно хотя бы при одном из этих отношений — умозаключение неправильное.

Упражнение 11

Произвести превращение и обращение следующих суждений.

1. Ни один марксист не является идеалистом.

2. Некоторые философы не являются диалектиками.

3. Все студенты — учащиеся.

4. Некоторые науки — классовые.

Упражнение 12

Проверьте правильность следующих умозаключений.

1. Все млекопитающие — позвоночные животные. Следовательно, ни одно беспозвоночное животное не является млекопитающим.

2. Некоторые киты являются дельфинами. Следовательно, некоторые животные, не являющиеся дельфинами, не киты.

3. Некоторые юристы не являются адвокатами. Следовательно, некоторые адвокаты не суть не юристы.

4. Некоторые юристы — адвокаты. Следовательно, некоторые адвокаты не суть не юристы,

Упражнение 13

Является ли правильным рассуждение Аристотеля:

“... Если истинно, что кто-то есть человек и не-человек, то ясно, что истинно также то, что он не есть ни человек, ни не человек...” (Аристотель. Метафизика // Соч. В 4 т. М., 1976. Т. 1. С. 131).