Георгий Рузавин - Логика и аргументация: Учебн. пособие для вузов.

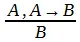
Горизонтальная черта здесь отделяет заключение от посылок. В качестве посылок выступают антецедент А и сама импликация А → В, заключением служит консеквент импликации. Таким образом, это правило разрешает нам отделить заключение от его посылок как самостоятельное знание. Так, в математике мы постоянно формулируем теоремы без указания тех посылок, из которых они выведены. Если при доказательстве ограничиваются только правилом отделения, тогда для этого необходимо убедиться в истинности посылок и правильности логического вывода. Поскольку в математике посылками служат в конечном счете аксиомы, принимаемые истинными без доказательства, постольку само доказательство сводится к проверке правильности логического вывода. В эмпирических науках, кроме того, необходимо обосновать истинность посылок, которыми могут служить различного рода допущения (эмпирические законы или обобщения, гипотезы, принципы, постулаты или даже целые теории).

Правило подстановкиразрешает вместо любой переменной в исчислении высказываний подставлять любое другое высказывание, но для того чтобы получить истинное высказывание в качестве заключения, необходимо, чтобы исходная формула была истинной.

Весьма простая система аксиом для исчисления высказываний была построена Б. Расселом и А.Н. Уайтхедом, а затем усовершенствована Д. Гильбертом. Она состоит из четырех аксиом:

1) x ∨ х → х.

2) х → х ∨ у.

3) x ∨ y → y ∨ x.

4) (х → у) → ((z ∨ x) → (z ∨ у)).

Аксиома 1 утверждает, что высказывание истинно, если дизъюнкция этого высказывания с самим собой истинна.

Аксиома 2 означает, что когда высказывание истинно, то к нему можно присоединить любой - истинный или ложный - дизъюнктивный член, так как дизъюнкция будет истинной, если один из членов будет истинным высказыванием.

Аксиома 3 представляет собой закон коммутативности для дизъюнкции.

Аксиома 4 утверждает, что в случае истинности импликации к ее антецеденту и консеквенту можно присоединить любой дизъюнктивный член, ибо он не повлияет на истинность импликации. Нетрудно заметить, что во всех формулах, выражающих аксиомы, можно заменить импликацию эквивалентным выражением: (х → у) (¬ ↔ х ∨ у). Обычно для формулировки аксиом используются две логические операции, так как для выражения сложных высказываний их достаточно.

Опираясь на эти аксиомы, с помощью указанных выше правил вывода можно вывести другие истинные высказывания логики высказываний. При аксиоматическом подходе мы не обращаемся к содержательным способам установления истинности высказываний, а, предполагая аксиомы истинными, с помощью правил отделения и подстановки выводим другие истинные заключения. Этот подход можно сделать чисто формальным, если рассматривать аксиомы как исходные формулы, а логические правила вывода как правила преобразования одних формул в другие. Именно так осуществляется формальный вывод и доказательство в математике, но это занимает много времени и требует особого внимания. Однако с помощью производных правил вывода и ранее доказанных теорем процесс формального доказательства можно ускорить, хотя математики на практике не обращаются к формальным доказательствам, пока не сталкиваются с противоречиями либо парадоксами или пока не возникает необходимость в тщательной проверке всех шагов доказательства.

Интересно отметить, что если запрограммировать процесс доказательства теорем, то можно убедиться, что компьютер сравнительно несложные формальные доказательства осуществляет быстрее и точнее человека, подобно тому как он выполняет действия над числами. Преимущество человека над вычислительной машиной выражается не только в понимании совершаемых им действий, но также в том, что он выполняет соответствующие действия крупными блоками, тогда как машина должна осуществить каждый шаг отдельно. Вместе с тем, благодаря огромной скорости быстродействия машина имеет значительное преимущество перед человеком именно при осуществлении рутинных операций и процессов, к которым относятся действия над числами и несложные логические и математические доказательства.

Процессы логического вывода и доказательства имеют много общего с рассуждениями в естественном языке, где также выводят одни высказывания из других, но, правда, при этом явно не указывают логические правила вывода, которыми пользуются, предполагая их известными. Именно это обстоятельство заставило логиков строить исчисления, напоминающие выводы в естественном языке. Нередко поэтому их называют натуральными выводами. Из этих исчислений наиболее известным и признанным считается система натурального вывода, построенная Г. Генценом, появившаяся в 1934 г. Хотя доказательства, основанные на выводе, применял еще Евклид в своих "Элементах" (геометрии), но в логике они стали анализироваться значительно позднее. Трудность здесь состоит в том, что рассуждения, которые осуществляются с помощью естественного языка, трудно переводятся на искусственный язык логики.

Рассуждения проводятся на естественном языке, но когда возникают трудности и неясности, тогда приходится обращаться к их логическому анализу. Такой анализ предполагает перевод с естественного языка на язык логики, в результате чего все связи между предложениями естественного языка заменяются логическими коннекторами (связками), смысл которых точно задан с помощью определений. Так, грамматический союз "и" в логике отображается конъюнкцией, союз "или" - дизъюнкцией и т.д. Но при этом иногда возникает несоответствие между предложениями естественного языка и соответствующими им логическими высказываниями. Мы уже говорили о том, что использование в логике операции дизъюнкции, соответствующей союзу "или" в естественном языке, часто наталкивается на сопротивление, потому что в логике этот союз рассматривается только в более широком, включающем смысле, тогда как в обычной речи или даже в науке он нередко используется в исключающем смысле. Правда, в принципе, исключающий смысл союза "или" в форме "либо - либо" можно выразить с помощью включающего "или" и некоторых других логических операций.

Гораздо больше трудностей, как мы видели, возникает с использованием операции импликации для выражения условных суждений, споры по поводу которого идут до сих пор. Даже такая сравнительно простая операция, как конъюнкция, иногда не передает всех нюансов использования союза "и" в естественном языке. В самом деле, хотя в силу закона коммутативности, конъюнкции (А ∧ В) и (В ∧ А) являются эквивалентными, тем не менее в естественном языке они не всегда воспринимаются такими. Например, предложение "Маша вышла замуж и родила ребенка" и предложение "Маша родила ребенка и вышла замуж" понимаются как неравнозначные с точки зрения последовательности событий во времени. Но это различие не может быть выражено адекватно на языке исчисления высказываний. Многие ограничения этого исчисления могут быть сняты с помощью построения более сильных средств логического анализа, в частности, например, в логике предикатов. Однако формализация никогда не может исчерпать всего богатства и возможностей постоянно совершенствующегося и развивающегося естественного языка.