Вячеслав Кириллов - Логика: учебник для юридических вузов

Значение выделяющих и исключающих суждений состоит в том, что положения, выраженные в форме этих суждений, характеризуются точностью и определенностью, что исключает их неоднозначное понимание. Именно поэтому ряд научных положений, а также статей международных документов, законов государства, статей уголовного, уголовно-процессуального и других кодексов выражен в форме выделяющих или исключающих суждений. Например, в Конституции Российской Федерации статьи 118 (часть 1) и 123 (часть 2) гласят: «Правосудие в Российской Федерации осуществляется только судом», «Заочное разбирательство уголовных дел в судах не допускается, кроме случаев, предусмотренных федеральными законами».

1. Какие суждения называются выделяющими? Могут ли быть выделяющими единичные, частные и общие суждения? Приведите их схемы.

2. Какие суждения называются исключающими? Приведите схему исключающего суждения.

В логических операциях с суждениями возникает необходимость установить, распределены или не распределены его термины — субъект и предикат. Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема.

Рассмотрим, как распределены термины в суждениях А, Е, I, О.

Суждение А (Все S есть Р). «Все студенты нашей группы ( S) сдали экзамены ( Р)». Субъект этого суждения («студенты нашей группы») распределен, он взят в полном объеме: речь идет о всех студентах нашей группы. Предикат этого суждения не распределен, так как в нем мыслится только часть сдавших экзамены. Не все сдавшие экзамены — студенты нашей группы.

Распределенность терминов в суждении принято изображать в круговых схемах. Распределенность субъекта и предиката в общеутвердительном суждении изображена на схеме 24.

Таким образом, в общеутвердительных суждениях S распределен , Р не распределен . Однако в общеутвердительных суждениях, субъект и предикат которых имеют одинаковый объем, распределен не только субъект, но и предикат. К таким суждениям относятся общевыделяющие суждения, а также определения, подчиняющиеся правилу соразмерности (схема 25).

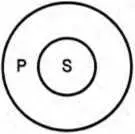
Схема 24

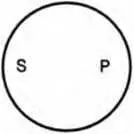
Схема 25

Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы ( S) не является неуспевающим ( Р)». И субъект, и предикат взяты в полном объеме. Объем одного термина полностью исключается из объема другого: ни один студент нашей группы не входит в число неуспевающих, и ни один неуспевающий не является студентом нашей группы. Следовательно, в общеотрицательных суждениях и S, и Р распределены (схема 26).

Суждение I (Некоторые S есть Р). «Некоторые студенты нашей группы ( S) — отличники ( Р)». Субъект этого суждения не распределен, так как в нем мыслится только часть студентов нашей группы, объем субъекта лишь частично включается в объем предиката: только некоторые студенты нашей группы относятся к числу отличников. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники — студенты нашей группы.

Следовательно, в частноутвердительном суждении ни S, ни Р не распределены (схема 27).

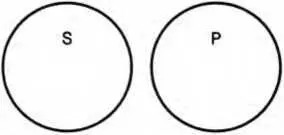
Схема 26

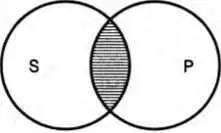
Схема 27

Исключение из этого правила составляют частновыделяющие суждения, предикат которых полностью входит в объем субъекта. Например: «Некоторые города, и только города ( S), являются столицами ( Р)». Здесь понятие «столица» полностью входит в объем понятия «города». Субъект такого суждения не распределен, предикат распределен (схема 28).

Суждение О (Некоторые S не есть Р). «Некоторые студенты нашей группы (S) не отличники (Р)». Субъект этого суждения не распределен (мыслится лишь часть студентов нашей группы), предикат распределен, в нем мыслятся все отличники, ни один из которых не включается в ту часть студентов нашей группы, которая мыслится в субъекте. Следовательно, в частноотрицательном суждении S не распределен, Р распределен (схема 29).

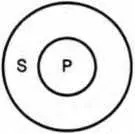
Схема 28

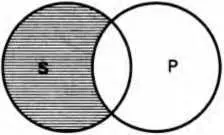
Схема 29

Приведем таблицу распределенности терминов, обозначив распределенность термина знаком +, нераспределенность знаком —.

Таблица 1

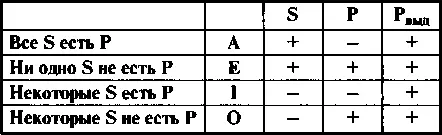
Из таблицы видно, что субъект распределен в общих ( Аи Е) и не распределен в частных суждениях ( Iи О). Предикат распределен в отрицательных ( Еи О) и не распределен в утвердительных суждениях ( Аи I). В выделяющих суждениях предикат распределен .

Суждения делятся на сравнимые и несравнимые.

Несравнимымиявляются суждения, имеющие разные субъекты или предикаты. Таковы, например, два суждения: «Некоторые студенты первокурсники» и «Некоторые студенты заочники».

Сравнимымиявляются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором. Обычно их называют суждениями одинаковой материи. Например: «Все американские индейцы живут в резервациях»; «Некоторые американские индейцы не живут в резервациях». Отношения устанавливаются только между сравнимыми суждениями.

Эти отношения обычно рассматриваются с помощью схемы, называемой логическим квадратом(схема 30). Его вершины символизируют простые категорические суждения — А, Е, I, О; стороны и диагонали — отношения между суждениями.

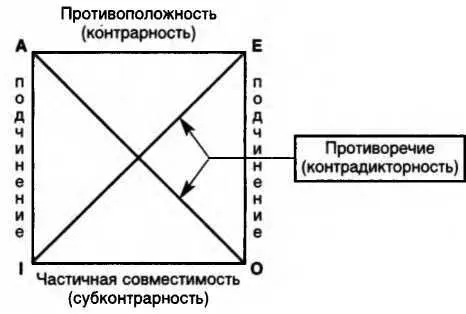
Схема 30

Среди сравнимых различают совместимые и несовместимые суждения.