Дмитрий Гусев - Логика. Учебное пособие

Между понятиями, а вернее между их объемами, существуют определенные отношения, знание которых является в логике одним из наиболее важных (можно сказать, что виды отношений между понятиями в логике – это примерно то же самое, что в математике таблица умножения). Обычно понятия делят на сравнимые( например, Москва и столица России, писатель и россиянин, город и населенный пункт, лев и тигр, горячая вода и холодная вода, высокий человек и невысокий человек ) и несравнимые(например, пингвин и кирпич, треугольник и президент, учебное заведение и небесное тело, спортсмен и город, книга и небоскреб, растение и государство ).

Сравнимые понятия бывают совместимымии несовместимыми. Совместимыминазываются понятия, объемы которых имеют общие элементы, каким-либо образом соприкасаются. Например, понятия спортсмен и американец совместимые, т. к. их объемы имеют общие элементы, или объекты: есть такие спортсмены, которые являются американцами и, наоборот, есть такие американцы, которые являются спортсменами. Несовместимыминазываются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Например, понятия треугольник и квадрат являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом и наоборот.

Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения.

Понятия находятся в отношении равнозначностив том случае, если их объемы полностью совпадают. Например, равнозначными будут поняти я квадрат и равносторонний прямоугольник , т. к. любой квадрат – это равносторонний прямоугольник, а любой равносторонний прямоугольник – это квадрат. В логике принято изображать отношения между понятиями с помощью круговых схем Эйлера (известный математик XVIII века): одно понятие, а вернее его объем, изображается одним кругом, а второе, т. е. его объем – другим. Взаимное расположение этих кругов на схеме (они могут полностью совпадать или пересекаться, или не соприкасаться, или один круг располагается внутри другого) и показывает то или иное отношение между понятиями. Так отношение равнозначности между понятиями квадрат и равносторонний прямоугольник изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают:

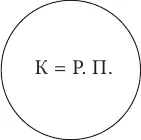
Понятия находятся в отношении пересечениятогда, когда их объемы совпадают только частично. Например, пересекающимися будут понятия школьник и спортсмен : есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий):

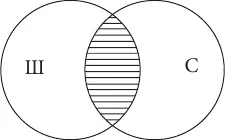
Понятия находятся в отношении подчиненияв том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия карась и рыба , т. к. все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим – родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого:

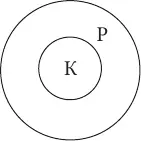
Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.

Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.

Понятия находятся в отношении соподчинениятогда, когда их объемы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия сосна и береза являются соподчиненными: ни одна сосна не может быть березой и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дерево. На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами:

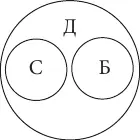
Понятия находятся в отношении противоположностив том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия высокий человек и низкий человек (третьим или переходным вариантом между ними будет понятие человек среднего роста ). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах»:

Поскольку объемы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью березы, а береза – противоположностью сосны: это просто разные деревья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека и наоборот. Так же противоположными будут понятия темная комната и светлая комната, горячая вода и холодная вода, белый лист и черный лист, глубокая речка и мелкая речка и т. п.

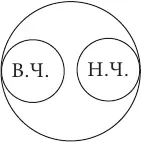
Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий, между противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия высокий человек и невысокий человек. В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и низкий человек , и человек среднего роста – это невысокий человек. На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия: