Валентин Асмус - Учение логики о доказательстве и опровержении

Мы рассмотрели две составные части доказательства: доказываемый тезис и основания доказательства. Мы видели, что главная задача доказательства — сделать непреложной либо истинность доказываемого, либо ложность опровергаемого. Мы видели также, что истинность доказываемого или ложность опровергаемого тезиса не могут быть обнаружены непосредственно. Чтобы убедиться в истинности доказываемого тезиса, следует указать истинное основание, признав которое истинным, мы с необходимостью должны признать истинным также и доказываемый тезис.

Однако, хотя указание истинных оснований для выяснения истинности доказываемого тезиса необходимо, но одним лишь этим мы ещё не достигаем цели доказательства. Только в немногих случаях указание истинных оснований даёт истинность доказываемого тезиса сразу, в виде непосредственного вывода. Так, если требуется доказать, что некоторые из равных между собой углов — прямые углы, то для доказательства истинности этого утверждения достаточно сослаться, как на основание, на истину о том, что все прямые углы равны между собою. Из этого основания сразу, непосредственно, по законам одной лишь логики (а именно — согласно правилам обращения) получается истинный вывод, что некоторые из равных между собой углов — прямые.

Но в огромном большинстве случаев знания истинных оснований, ведущих к признанию истинности тезиса, недостаточно. Необходимо кроме того показать, какова связь, необходимо ведущая от истинности данных оснований к истинности обусловленного ими тезиса. Связь эта во многих случаях непосредственно не видна и требует выяснения. Так, если ученик знает все определения, все аксиомы и все теоремы, из истинности которых, как из оснований, выводится истинность теоремы Пифагора, это ещё не значит, что ученик знает доказательство теоремы Пифагора. Для знания доказательства требуется, чтобы ученик знал, какова связь между всеми известными ему порознь основаниями теоремы Пифагора,— другими словами, какова последовательность оснований и выводов из оснований, необходимо ведущая к признанию истинности доказываемого в этой теореме положения.

Последовательность, или связь оснований и выводов из оснований, имеющая результатом необходимое признание истинности доказываемого тезиса, называется способом доказательства у или демонстрацией. Демонстрация есть не составная часть доказательства, но третья, наряду с доказываемым тезисом и основаниями, логическая характеристика доказательства.

Из этого определения демонстрации видно её отличие от составных частей доказательства— тезиса и основания. И тезис и каждое из оснований — положение об удостоверенном факте, определение, аксиома, ранее доказанное положение науки — представляют собой отдельное суждение. Напротив, демонстрация никогда не есть ни отдельное суждение, ни простая сумма отдельных суждений. Демонстрация всегда есть логическая связь суждений, приводящая к определённому логическому результату. Демонстрация это более или менее длинная цепь умозаключений у посылками которых являются основания данного доказательства, а последним заключением — доказываемый тезис у который, таким образом, удостоверяется в качестве истинного.

Так, при доказательстве теоремы евклидовой геометрии о сумме внутренних углов треугольника (см. рис. 2) мы сначала продолжаем сторону треугольника АВС, например сторону АС до точки Е. Затем проводим из точки С прямую CD, параллельную АВ и по одну с ней сторону от прямой АС. Затем мы рассуждаем следующим образом. Прямая ВС пересекает параллельные (по построению) прямые АВ и CD. Следовательно, углы АВС и BCD будут равны как внутренние накрест лежащие. Прямая АС пересекает те же—параллельные по построению — прямые АВ и CD. Следовательно, углы ВАС и DCE равны как соответственные. Угол ВСЕ, представляющий сумму углов BCD и DCE, равен сумме двух внутренних углов треугольника (АВС и ВАС), так как угол BCD равен углу АВС, а угол DCE равен углу ВАС. Прибавим к углу ВСЕ угол ВСА — третий внутренний угол треугольника АВС. Тогда сумма углов DCE, BCD и ВСА будет равна сумме внутренних углов данного треугольника: углов ВАС, АВС и ВСА. Но так как сумма углов ВСЕ (равного сумме углов ВАС и АВС) и ВСА равна сумме двух смежных углов, а эта сумма равна двум прямым углам, то сумма внутренних углов ВАС, АВС и ВСА в треугольнике АВС также равна двум прямым.

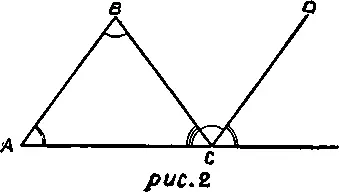
Всё в целом это рассуждение — демонстрация. Основания доказательства не выделяются в группу положений, отдельных от демонстрации, но появляются каждое на том месте, какое определяется для него логической связью всех звеньев демонстрации.

Так как демонстрация — порядок связи между основаниями и тезисом— порядок, непросто усматриваемый из оснований, но такой, который ещё должен быть найден, то доказательство одного и того же положения науки может быть более или менее сложным или простым, громоздким или кратким и т. д. Самый порядок, план доказательства может варьироваться.

Связь оснований, ведущая к усмотрению истинности доказываемого тезиса,— не единственная. А так как связь эта не дана вместе с самими основаниями, но ещё должна быть открыта, выяснена, найдена, то доказательство есть творческая задача науки, которая творческими же средствами и решается.

В ряде частных случаев задача доказательства оказывается настолько сложной, что разрешение её требует от учёных огромных усилий на протяжении целых десятилетий или даже столетий. До сих пор не найдено доказательство теоремы Ферма о том, что уравнение x n= y n+z nне может иметь решений для всех целых значений n больших дЕух. В течение почти двух с половиной тысячелетий оставалось недоказанным существование атома, пока успехи новейшей экспериментальной и теоретической физики не принесли, наконец, это доказательство. Гениальная догадка Джордано Бруно о существовании планет, обращающихся вокруг других звёзд, получила доказательное подтверждение только в последние десятилетия. Во всех этих случаях учёным пришлось приложить немало усилий для доказательства того, что могло быть доказано лишь при определённых условиях развития наблюдения, эксперимента и теоретического анализа.

С другой стороны, там, где задача доказательства успешно разрешалась, пути и средства её разрешения у разных учёных были неодинаковы. Уже античная математика знала не одно единственное доказательство теоремы Пифагора, а целый ряд таких доказательств. И это типично для доказательства. Доказываемый тезис — один, логические законы мышления — одни, но способы, ведущие к признанию истинности тезиса, могут быть разные. Способы эти определяются: 1) основаниями, из которых выводится тезис, 2) связью между основаниями и тезисом. Связь эта не видна из оснований, отдельно взятых. Она находится посредством рассмотрения отношений между доказываемым тезисом и тем, что уже ранее было доказано.