Eduardo Lopez - Космос становится больше. Хаббл. Расширение Вселенной

Часто великие ученые выступают и мыслителями, что проявляется в их любопытстве к темам, не касающимся их специальности. Широкий спектр интересов Хаббла свидетельствует о том, что он был именно таким ученым. В 1949-м, на следующий год после сердечного приступа, Эдвин с Грейс поехали в Европу — в этот раз им удалось посетить пещеру Ласко. Эта пещера находится в Монтиньяке, недалеко от Брив-ла-Гайард, то есть в самом сердце Франции, поэтому любопытство Хаббла достойно восхищения. Слава шла впереди ученого, и благодаря этому у него было два прекрасных гида — те самые молодые люди, которые открыли пещеру 10 десять лет назад (к описываемому времени они превратились в зрелых 27-летних мужчин). Эдвина и Грейс повели по всем галереям, закрытым для посещений. Аббат Брейль, высший авторитет по искусству палеолита во Франции, назвал пещеру французской Альтамирой и относил рисунки к ориньякскому периоду, то есть их древность составляла от 30 000 до 38 000 лет. Сегодня известно, что рисунки относятся к мадленской культуре, то есть были сделаны 17 000-18 600 лет назад. В зале быков Хабблы восхитились совершенством фигур: единорог, лошади, большой бык, олени, корова, медведь были нарисованы с невероятным мастерством. На глубине 800 м стены пещеры покрывали бесчисленные рисунки. Грейс записала в своем дневнике: «Общее впечатление было во много раз сильнее, чем можно было ожидать».

Изображение из пещеры Ласко. Хаббл с женой посетили ее в 1949 году.

Его мнение в рассматриваемых им проблемах всегда было безупречным. Каждая его статья становилась классической.

Аллан Сандаж о Хаббле

Эдвин и Грейс совершили еще одно путешествие в Европу, посетив Лондон, Эдинбург, Париж, Ласко, Кембридж... В Лондоне они познакомились с королевой Елизаветой I, которой тогда было 26 лет. Также супруги навестили Хойла, Джинса и всех своих добрых британских друзей. После возвращения Эдвин был полон энергии и готовности посвятить себя исследованиям с помощью телескопа в May нт-Пал омаре, который был словно специально задуман для него. Хаббл уже представлял, как он появится в свете, как будет показывать свою медаль за гражданские заслуги, как будет восхищать всех своей британской невозмутимостью... Он заказал херес у своего английского поставщика в Лос-Анджелесе, чтобы выпить за выздоровление...

На следующий день, 28 сентября 1953 года, Эдвин Пауэлл Хаббл умер от тромбоза сосудов головного мозга. Ему исполнилось 64 года. Смерть была быстрой и безболезненной — именно такой, как он мечтал. Траурной церемонии не было — ни торжественной, ни чисто семейной. Грейс исполнила последнее желание мужа, и сегодня никому не известно, где покоятся его останки.

Тот, кто так ценил успех при жизни, после смерти пренебрег им.

В классической механике жидкостей есть две базовые формулы, хорошо известные студентам: уравнение постоянства и уравнение Бернулли.

Уравнение постоянства, которое представляет собой не что иное, как выражение сохранения массы, выглядит так:

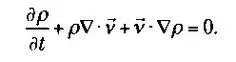
Но перепадов плотности, согласно космологическому принципу, быть не может. Плотность зависит только от времени, поэтому третье слагаемое можно убрать:

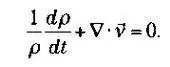
Первое слагаемое зависит только от времени, значит второе тоже может зависеть только от времени при помощи неизвестной функции, которую можно назвать 3H(t). Но

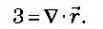
Затем мы можем написать:

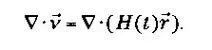
Так как H(t) — только функция времени, в формулу можно также включить дивергенцию. Решение представляет собой уравнение типа

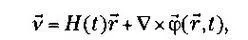
где векторная функция φ — некая неизвестная функция. Это выражение действительно является решением дифференциального уравнения, так как дивергенция ротора любого вектора равна нулю. Она не может зависеть от позиционного вектора — только от его модуля, иначе был бы нарушен принцип изотропии. Но ротор такой функции равен нулю, поэтому мы получаем

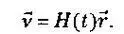
Это эквивалент формулы Хаббла с уточнением: скорость должна быть чистым расширением. Функция H(t) остается неизвестной, для ее определения нужно использовать другие уравнения, а лучше — релятивистские уравнения сохранения импульса и энергии, которые выходят за рамки нашего приложения. H(t) может принимать положительные, отрицательные, нулевые значения, знак может меняться с течением времени. Наблюдения показывают, что сегодня H 0положительна. Наблюдается расширение.

Рассмотрим альтернативное рассуждение, которое кажется более простым и основано на уравнении Бернулли. Этот ученый объяснил нам много любопытного в поведении жидкостей. Его знаменитая формула в своей самой известной форме выглядит так:

p+1/2pv2 = постоянная,

где р — давление. Эта формула выполняется, когда в разных точках жидкости гравитация одинакова. Если имеются изменения гравитации, надо добавить в формулу потенциальную гравитационную энергию. Нам не обязательно учитывать давление, так как космологический принцип говорит, что давление во всех точках одинаково; его значение может перейти

ко второму члену и добавиться к постоянной. Потенциальная энергия на единицу объема записывается как ~(GM l)/r, где масса М = р4лг*/3, затем

-4/3πGp²r² + 1/2pv²

Заметьте, что М(r) — масса, содержащаяся в сфере с радиусом r.

Чтобы найти величину постоянной, рассмотрим «здесь» с r = 0. Мы не видим скорости расширения. Очевидно, что r = 0, постоянная второго члена равна нулю. Таким образом, получаем

v = (8/3πGp) ½r = H 0r

Мы не только получили закон Хаббла, но и рассчитали величину H 0:

H 0= √(8/3πGp).

Об этом ли значении говорят релятивистские модели? Не совсем — это величина, соответствующая критической, или плоской, Вселенной с нулевой кривизной. Так как мы исходили из классических уравнений, сложно претендовать на большую точность. Формулировки, представленные в этом приложении, конечно же, очень поверхностны, но они иллюстрируют то, что закон Хаббла — прямое следствие космологического принципа и его мог бы открыть даже студент-физик. Естественно, апостериори все открытия выглядят очевиднее.