Чарльз Сейфе - Ноль: биография опасной идеи

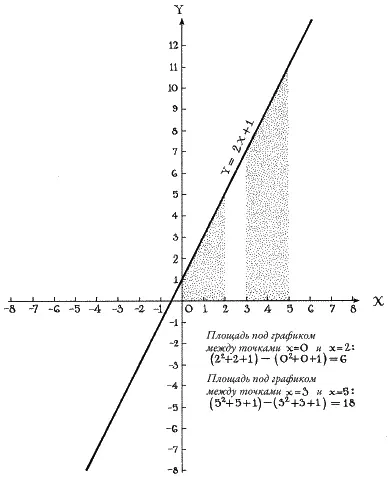
Рис. 27. Чтобы узнать площадь под кривой y = 2x + 1, используйте формулу y = x 2+ x + 1

Математический анализ — это комбинация этих двух инструментов, дифференцирования и интегрирования, в одной упаковке. Хотя Ньютон нарушил некоторые очень важные математические правила, заигрывая с нолем и бесконечностью, математический анализ давал настолько мощные методы вычислений, что ни один математик не смог его отвергнуть.

Природа говорит уравнениями. В этом странное совпадение. Правила математики были выстроены на основании подсчета овец и измерения земельных участков, однако те же самые правила управляют Вселенной. Законы природы описываются уравнениями, а уравнения в определенном смысле — всего лишь инструменты, используя которые, вы вводите числа и получаете другое число. Древние знали несколько этих уравнений-законов, вроде закона рычага, но с началом научной революции уравнения-законы стали появляться отовсюду. Третий закон Кеплера описывал время, которое нужно планетам для обращения по орбите: r 3/ t 2= k , где t — время, r — расстояние и k — константа. В 1662 году Роберт Бойль показал, что если взять запечатанный сосуд с газом внутри и начать газ сжимать, то давление внутри возрастет: давление, умноженное на объем, есть константа: pυ = k , где p — давление, v — объем, k — константа. В 1676 году Роберт Гук вычислил силу действия пружины. Она равна отрицательной константе, умноженной на расстояние: f = –kx , где f — сила, x — расстояние, на которое растянута пружина, и k — константа. Эти ранние уравнения-законы были очень хороши для выражения простых зависимостей, однако уравнения имели ограничения — их постоянство, что не позволяло им быть универсальными.

Например, возьмем знаменитое уравнение, с которым все мы знакомимся в школе: скорость, умноженная на время, дает расстояние. Оно показывает, как далеко (на сколько миль — x ) вы продвинетесь, если будете бежать с постоянной скоростью v в час на протяжении t часов: υt = x. Это уравнение очень полезно, когда вы подсчитываете, сколько времени займет путь от Нью-Йорка до Чикаго на поезде, который едет со скоростью ровно 120 миль в час. Однако сколько предметов на самом деле двигаются с постоянной скоростью, как поезд в этом математическом примере? Уроните мяч, и окажется, что он падает все быстрее и быстрее. В данном случае уравнение x = vt попросту неверно. В случае падающего мяча x = gt 2 / 2, где g — ускорение, вызванное гравитацией. С другой стороны, если вы приложите к мячу увеличивающуюся силу, может оказаться, что x = at 3 / 3. Равенство расстояния скорости, умноженной на время, — это не универсальный закон, он действует не при всех условиях.

Исчисление позволило Ньютону объединить все эти уравнения в один великий свод законов — законов, приложимых во всех случаях, при всех условиях. Впервые наука смогла увидеть универсальные законы, лежащие в основе всех этих мелких полузаконов. Несмотря на то, что математики знали о глубинном пороке анализа, связанном с математикой ноля и бесконечности, они быстро восприняли новые математические инструменты. Дело в том, что природа говорит не обычными уравнениями. Она говорит дифференциальными уравнениями, и математический анализ — инструмент, который нужен, чтобы их создавать и решать.

Дифференциальные уравнения отличаются от обычных, с которыми все мы знакомы. Обычное уравнение подобно машине: вы скармливаете машине числа, и она выбрасывает ответ. Дифференциальное уравнение тоже похоже на машину, но на этот раз вы вводите в машину уравнения, а получаете новые уравнения. Загрузите уравнение, описывающее условия проблемы (движется ли мяч с постоянной скоростью или на мяч действует сила), и в результате получите уравнение, в котором закодирован ответ, который вы ищете: двигается ли мяч по прямой или по параболе. Одно дифференциальное уравнение управляет всем неисчислимым количеством уравнений-законов. И в отличие от мелких уравнений-законов, которые то выполняются, то нет, дифференциальное уравнение верно всегда. Это универсальный закон, возможность заглянуть в механизм природы. Математический анализ Ньютона — его метод флюксий — сделал именно это: связал вместе такие концепции, как позиция, скорость, ускорение. Когда Ньютон обозначил положение функцией времени x, он понял, что скорость — это просто флюксия (современные математики называют ее производной от положения по времени: x́), а ускорение — всего лишь производная от скорости по времени: x˝ Переход от положения к скорости и к ускорению и обратно так же прост, как дифференцирование или интегрирование.

Имея в руках такой инструмент, Ньютон смог создать простое дифференциальное уравнение, описывающее движение всех тел во Вселенной: F = mx˝, где F — сила, действующая на тело, а m — его масса. (На самом деле это не вполне универсальный закон, поскольку уравнение верно, только когда масса объекта постоянна. Более общая версия закона Ньютона [29] Именно так закон формулировался Ньютоном, а более привычная нам формулировка (сила равна массе, умноженной на ускорение) была придумана для школьников, которые начинают изучать механику раньше анализа. выглядит так: F = ṕ, где p — количество движения, или импульс тела. Конечно, уравнения Ньютона были со временем усовершенствованы множеством ученых, в том числе Эйнштейном.)

Если у вас имеется уравнение, которое говорит вам о силе, приложенной к телу, дифференциальное уравнение точно сообщит вам, как тело движется. Например, мяч в свободном падении движется по параболе, в то время как пружина без трения вечно раскачивается туда и сюда, а под действием трения медленно останавливается (рис. 28). Какими бы разными ни казались эти исходы, все они описываются одним и тем же дифференциальным уравнением.

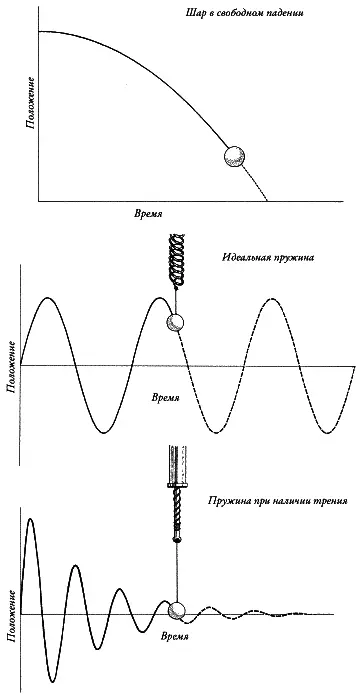
Рис. 28.Различные движения, описываемые одним и тем же дифференциальным уравнением

Точно так же, если вам известно, как движется тело — будь это мячик или гигантская планета, — дифференциальное уравнение скажет вам, какого рода сила к нему приложена. (Триумф Ньютона заключался в выведении уравнения, описывавшего силу притяжения и форму орбит планет. Раньше предполагалось, что сила была пропорциональна 1 / r 2, и когда из дифференциальных уравнений Ньютона были получены эллиптические орбиты, люди стали верить в правоту Ньютона.) Несмотря на возможности анализа, ключевая проблема сохранялась. Работы Ньютона основывались на очень шатком фундаменте — делении ноля на самого себя. Труды его соперника имели тот же недостаток.