Антонио Дуран - Истина в пределе. Анализ бесконечно малых

На пятистах страницах «Курса анализа» также приводятся определения непрерывной функции, комплексного числа, формулируются критерии сходимости рядов и так далее.

Работы Коши о сходимости рядов вызвали большое возбуждение. Рассказывают, что после собрания Французской академии наук, где ученый изложил свои идеи о сходимости рядов, обеспокоенный Лаплас заперся у себя дома и не выходил, пока не проверил, что все ряды, использованные им в «Небесной механике», сходятся, и лишь тогда вздохнул с облегчением.

Коши планировал, что «Курс анализа» будет состоять из двух томов, но неблагоприятные отзывы заставили его отказаться от написания второго тома. Суть критики сводилась к тому, что книга, по мнению руководства Политехнической школы, не подходила для образования будущих инженеров. Поэтому Коши решил пересмотреть идею о публикации второго тома и вместо этого выпустил дополнение к «Курсу анализа», представлявшее собой краткое изложение его лекций. Первый том увидел свет в 1823 году под названием «Резюме лекций по исчислению бесконечно малых», где давалось современное определение производной как предела

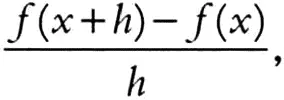
когда h стремится к 0.

Огюстен Луи Коши родился в 1789 году, спустя несколько месяцев после начала Великой французской революции. Он занимает почетное место среди ведущих математиков первой половины XIX века. Благодаря ему был сделан значимый шаг в сторону большей логической строгости математических рассуждений. Так, в статье Энциклопедии Британника о нем сказано: «Коши был одним из величайших математиков современности. Одним из наиболее значительных его достижений является четкость и строгость введенных им методов. Первый этап логической строгости, характерной для современной математики, берет начало в его лекциях и книгах по математическому анализу, написанных в 1820-1830 годах». Также всегда указывается, что он был разносторонне образованным человеком и интересовался классическими языками. Он был ревностным католиком и яростно защищал право Бурбонов на французский престол, дарованное Богом. «Его коллеги часто упрекали его в непреклонном ханжестве и агрессивном религиозном фанатизме»,- говорится об этом в уже упомянутой Энциклопедии Британника. Он был преподавателем Политехнической школы и членом Французской академии наук. По политическим мотивам ему пришлось покинуть Францию на период с 1830 по 1838 год. Умер Коши в 1857 году.

В «Резюме лекций по исчислению бесконечно малых» также приводится определение интеграла непрерывной функции

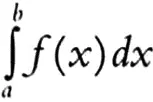
как предела сумм Коши:

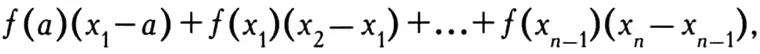
где a < х 1< х 2< … < x n-1 < b — разбиение интервала [а, b], а искомый интеграл рассчитывается как предел при разбиении интервала на отрезки, длины которых стремятся к 0.

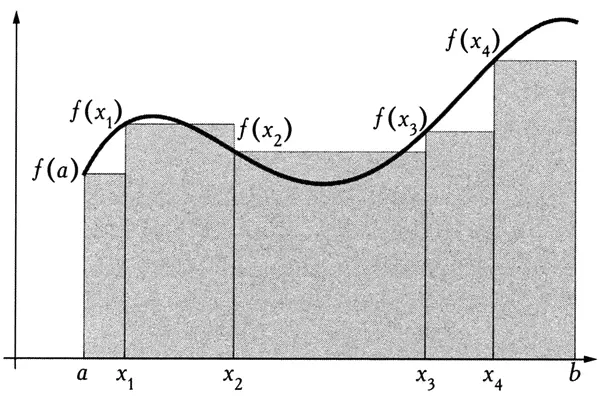
Как показано на иллюстрации, каждое слагаемое этой суммы соответствует площади прямоугольника, и мы можем выразить площадь подграфика функции с любой точностью.

Также в книге определяются и рассматриваются несобственные интегралы, главные значения несобственных интегралов и сингулярные интегралы, основная теорема анализа, формула Тейлора и так далее. Коши продемонстрировал функцию

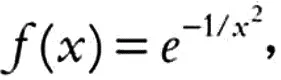
ряд Тейлора для которой в точке 0 сходится, но отличается от функции в окрестности нуля. Это доказывает невозможность выстраивания анализа бесконечно малых поверх прочной основы, предложенной Лагранжем.

Мы не будем говорить о других работах Коши и резюме его лекций, а расскажем о значимости его трудов в формировании основы анализа бесконечно малых.

Несомненно, его попытки логически обосновать анализ бесконечно малых были значимым этапом, но тем не менее не окончательным. Нильс Абель, великий норвежский математик, одним из первых обратил внимание на важность работ Коши, отметив их строгость и вместе с тем неполноту. Одновременно с этим он указал, в чем именно заключаются недостатки работ Коши. Это был очередной шаг вперед на пути, который полностью был пройден в середине XIX века с появлением работ Вейерштрасса. Окончательное и четкое определение вещественных чисел было дано еще два десятилетия спустя. Сам Абель в статье, опубликованной в 1826 году, доказал, что одна из теорем «Курса анализа» Коши «допускала исключения» (оцените дипломатичность формулировки!). Эта теорема Коши была не единственной, «допускающей исключения».

Нильс Хенрик Абель (1802-1829) был одним из наиболее ожесточенных противников отсутствия математической строгости: «В высшей математике, — писал он в 1826 году, — лишь некоторые предположения доказаны с неоспоримой строгостью. Неизменно встречается печальная привычка выводить общее из частного, и, несомненно, весьма заметно, что результатами подобных рассуждений чаще всего являются парадоксы». Поэтому неудивительно, что Абель изучал тексты Коши и ценил его стремление внести строгость и порядок в математику. «Коши упрям,- писал Абель, будучи в Париже в 1826 году,- и с ним нельзя договориться, но именно он сегодня лучше всех знает, как следует обращаться с математикой. Его работы удивительны, но достаточно запутаны. Сперва я ничего в них не понял, но теперь начинаю понимать их более ясно».

В статье о биноме Ньютона, опубликованной в 1826 году, он пишет: «Курс анализа» Коши следует прочитать всякому аналитику, который хочет действовать в своих математических исследованиях со всей строгостью».

Однако усилия Коши по приданию математическому анализу большей строгости были лишь очередным промежуточным этапом развития этой дисциплины. Доказательством этому служит то, что исследователи работ ученого не пришли к единому выводу об истинности или ошибочности его теорем. Это кажущееся противоречие вызвано тем, что определения, представленные Коши в «Курсе анализа», были неточными и нечеткими и порой допускали несколько толкований. Неоднозначность этих определений лучше всего объясняет Айвор Граттангиннес: «Достаточно сказать, что использованные им технические термины заслуживают внимания, и в теореме Коши, как и во всем его анализе, они применяются крайне свободно».