Gustavo Pineiro - У интуиции есть своя логика. Гёдель. Теоремы о неполноте.

а · (b - а) = (b + а) · (b - а)

мы сокращаем скобки (b - а) и делаем вывод, что а = b + а. Это ошибочно, потому что (b - а) равно 0 (поскольку а = b), а 0 нельзя делить. Если представить это в виде чисел и предположить, например, что а и b равны 2, переход от 5 к 6 соответствует тому, чтобы сказать, что из 2 · 0 = 4 · 0 (что истинно) следует 2 = 4.

Но как мы можем научить компьютер обнаруживать ошибки такого типа? Компьютер — это только машина; он не рассуждает, а слепо следует программе, записанной в его памяти. Для того чтобы компьютер мог проверить правильность математического рассуждения, необходимо перевести это рассуждение в последовательность высказываний, каждое из которых либо аксиома, либо выводится из предыдущих высказываний посредством применения точных и заранее установленных логических правил.

Рассмотрим пример математического доказательства, выраженного таким образом. Для начала нам нужны некоторые аксиомы, которые будут служить нам отправной точкой. В 1889 году, задолго до открытия парадокса Рассела, итальянский математик Джузеппе Пеано предложил набор аксиом, которые (как он предполагал) позволяют доказать все арифметические истины. Эти аксиомы основывались на операциях сложения (+), произведения (·), а также понятии последующего элемента (обозначаемого буквой S).

Пеано понимал, что последовательность натуральных чисел получается на основе числа 1 посредством повторного применения функции последующего элемента. Таким образом, 2 определяется как последующий элемент для 1, что обозначается S (1) = 2; 3, по определению, — последующий элемент для 2, то есть S (2) = 3; и так до бесконечности.

Для нашего примера достаточно взять две аксиомы Пеано, относящиеся к сложению.

Аксиома 1: каким бы ни было число х, х + 1 = S(x).

Аксиома 2: какими бы ни были числа х и у, S(x + у) = х + S(у).

В первой аксиоме говорится, что последующий элемент числа х всегда получается прибавлением к нему 1. Вторую аксиому можно воспринимать как (x+y) + 1 = x + (y +1). На основе этих двух аксиом докажем, что 4 = 2 + 2.

Логическая структура доказательства того, что 4*2 + 2. Стрелки показывают применения правил вывода.

Но действительно ли нужно доказывать, что 4 = 2 + 2? Разве это не очевидный факт? Хотя это действительно очевидно, по программе Гильберта любое истинное утверждение, не являющееся аксиомой, должно доказываться на их основе. За исключением высказываний, которые явно указаны как аксиомы, нет других утверждений, которые сами по себе считаются истинными.

Итак, докажем, что 4 = 2 + 2, но запишем рассуждение таким образом, чтобы его мог обработать компьютер. Добавим несколько комментариев, чтобы мы, люди, могли следить за идеей (см. схему).

1. S(x + у) = х + S(y) Аксиома 2.

2. S(2 + 1) = 2 + S(1) Подставили х=2 и у= 1 в аксиому 2.

3. S(2 + 1) = 2 + 2 Заменили S(1) на 2 в предыдущем шаге.

Комментарий: в следующих трех шагах представлено небольшое поддоказательство того, что 2 + 1 = 3; таким образом, в шаге 3 мы можем заменить S(2 + 1) на S(3).

4. х +1 = S(x) Аксиома 1.

5. 2 + 1 = S(2) Подставили = 2 в аксиому 1.

6. 2 + 1 = 3 В предыдущем шаге заменили 5(2) на З.

Комментарий: теперь мы можем заменить 5(2 + 1) на 3 в третьем шаге.

7. S( 3) = 2 + 2

8. 4 = 2 + 2 Заменили S(3) на 4 в предыдущем шаге.

Нужна ли такая точность для доказательства того, что два плюс два равно четыре? Да, это необходимо, если мы хотим, чтобы компьютер был способен проверять правильность рассуждений. Компьютер не думает; следовательно, мы должны вести его за руку, шаг за шагом показывая ему, используя заранее установленные правила, что именно мы сделали на каждом этапе рассуждений.

Действительный мир есть мир, постоянно изменяющийся. [...] Но такие изменения, независимо от их силы, никогда не разрушат истинности отдельного логического или арифметического закона.

Рудольф Карнап. «Философские основания физики»

Что будет делать компьютер, чтобы проверить, правильно ли наше доказательство? Для начала он возьмет первое высказывание и проверит, является ли оно аксиомой. Эта проверка происходит от символа к символу, точно так же как текстовый редактор проверяет орфографию, буква за буквой сверяя слова со словарем, загруженным в память компьютера.

Вспомним, что каждое высказывание должно либо быть аксиомой, либо выводиться из предыдущих высказываний. В нашем примере машина убедилась бы, что первое высказывание — это одна из аксиом в списке (первое высказывание должно быть аксиомой, его нельзя вывести из предыдущих высказываний, просто потому что их нет). Компьютер, конечно же, не понимает значения аксиомы, он только проверяет, что первое высказывание присутствует в списке, предварительно в него загруженном.

После первой проверки машина переходит ко второму высказыванию, S(2 + 1) = 2 + S(1), и проверяет, что это не аксиома (поскольку ее нет в списке). Тогда это второе высказывание должно сводиться к первому с помощью какого-либо логического правила. Чтобы осуществить эту проверку, в память компьютера должен быть загружен список правил логики, то есть правил, которые показывают, какие выводы можно сделать из определенных предпосылок (см. схему).

В случае нашего доказательства правило, позволяющее перейти от шага 1 к шагу 2, заключается в том, что если высказывание начинается с «какими бы ни были числа х и y...», то в следующем выражении буквы х и у могут быть свободно заменены любыми числами. В нашем примере буква х заменена числом 2, а у — числом 1.

Эти логические правила находятся вне арифметики, они справедливы для любой области математики, поэтому выражающие их высказывания называются универсально справедливыми высказываниями (или логическими аксиомами, поскольку они выражают правила логических рассуждений).

Мы уже упомянули одно из этих правил. Другие примеры: «если х = у, то у = х» и «если два числовых выражения равны, то любое из них может быть заменено на другое». Именно это — последнее — правило оправдывает переход от шага 2 к шагу 3, где S(1) заменяется на 2.

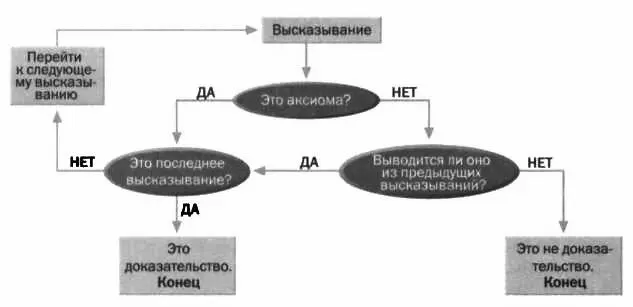
Схема механической проверки доказательства.

Но когда существует потенциально бесконечное число универсально справедливых высказываний, как мы можем загрузить их все в память компьютера? Если это нельзя сделать, то компьютер неспособен проверить справедливость любого рассуждения, и, следовательно, программа Гильберта оказывается неосуществимой. При этом ни один компьютер не способен содержать бесконечное число высказываний.

Как программа Гильберта, так и доказательство Гёделя предполагают, что все арифметические высказывания написаны на формальном языке с помощью заранее установленных символов. Существуют возможные варианты символов, один из наборов которых следующий.