Gustavo Pineiro - У интуиции есть своя логика. Гёдель. Теоремы о неполноте.

1. Р доказуемо, по гипотезе.

2. Выводится, что "не-<2=" Р" доказуемо, по правилу "а".

3. Следовательно, "не-Р=> Q" доказуемо, по правилу "б".

4. Не-P доказуемо, по гипотезе.

5. Из не-Р (пункт 4) и "не-Р =" Q" (пункт 3), по правилу вывода, выводится Q.

6. Следовательно, Q доказуемо.

Поскольку Q было произвольным высказыванием, можно сделать вывод, что любое высказывание доказуемо на основе аксиом. То есть любое высказывание доказуемо на основе противоречивого множества аксиом.

Заметим, что проделанные нами рассуждения чисто синтаксические и не затрагивают ни значения Р или Q, ни таких семантических понятий, как "истинно" или "ложно". Мы основывались только на синтаксических правилах логики и на виде высказываний. Таким типом аргументов Гёдель воспользовался для изложения доказательства своей теоремы.

Бертран Рассел в своем парадоксе на самом деле показал, что система аксиом, которую предложил Фреге, противоречива. Рассмотрим эту идею более подробно. Вспомним, что Рассел определил множество R, образованное всеми множествами, не являющимися членами самих себя.

Если R является членом самого себя, то выводится, что оно им не является. Это противоречие, которое возникает от предположения, что R — член самого себя, дает основание допустить: R не является членом самого себя. Но если предположить это, то логическим путем можно прийти к выводу, что все-таки является. Тогда получается, что R является членом самого себя. Парадокс Рассела на самом деле демонстрирует: существует такое высказывание, что и оно, и его отрицание доказуемы на основе аксиом Фреге. Другими словами, как уже говорилось, это демонстрирует противоречивость аксиом Фреге.

Как-то раз, читая лекцию для широкой публики, Бертран Рассел упомянул, что если множество аксиом противоречиво, то любое утверждение доказуемо на их основе. Рассел объявил об этом в семантическом виде, говоря, что исходя из ложной предпосылки можно доказать любую вещь. Аудитория сразу же предложила ученому доказать, что Смит (один из слушателей) является Папой Римским, исходя из ложной предпосылки о том, что 1 = 0. Рассел рассуждал так: если 1 = 0, то при прибавлении 1 к обоим членам мы делаем вывод, что 2 = 1. Теперь подумаем о множестве, образованном Смитом и Папой. У этого множества два члена, но так как 2 = 1, то мы можем сказать, что у множества только один член. То есть Смит и Папа — это одно и то же лицо.

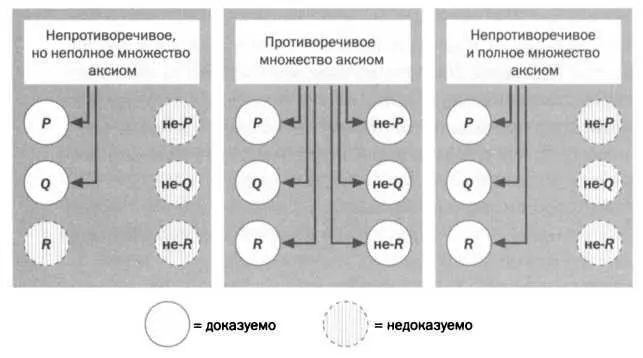
На основе противоречивого множества аксиом доказуемо что угодно. В связи с этим возникает новое синтаксическое понятие полноты. Множество аксиом является полным, если для любого высказывания либо оно, либо его отрицание (по крайней мере одно из них) доказуемо.

Тогда мы можем утверждать, что любое противоречивое множество аксиом является полным, поскольку при любом высказывании Р как Р, так и не-Р доказуемы. Но речь идет о тривиальной полноте, которая не дает никакой информации, поскольку абсолютно все доказуемо, даже те высказывания, которые противоречат сами себе, например "для любого х справедливо то, что х отличается сам от себя".

Более интересно рассмотреть множество аксиом, являющееся одновременно полным и непротиворечивым. Множество аксиом с такой характеристикой приблизилось бы к выполнению цели программы Гильберта. Действительно, если система непротиворечива, то ее высказывания истинны в каком-нибудь мире, а если она полна, то все истины, относящиеся к этому миру, доказуемы (см. схему).

Но в программе Гильберта искали аксиомы для арифметики, а не произвольного мира. Есть ли какой-нибудь синтаксический способ сформулировать эту цель? Да, такой способ есть.

Существуют некоторые арифметические высказывания, истинность или ложность которых можно проверить алгоритмически за конечное количество шагов, — интуиционисты могли бы считать их истинными или ложными без споров, в основном потому что они не затрагивают идею бесконечности (даже в потенциальном значении).

Например, следующие финитные высказывания

"2 + 3 = 5"

"3 х 7 = 21"

"45 делится на 9"

"2 — простое число"

истинны (во всех этих случаях мы рассматриваем мир натуральных чисел), а "2 х 3 = 10" — финитное и ложное. Высказывание "Любое четное число, большее 2, является суммой двух простых чисел" не является финитным, поскольку предполагает бесконечное число случаев. Действительно, это равносильно "4 — сумма двух простых чисел, и 6 — сумма двух простых чисел, и 8 — сумма двух простых чисел (и так далее)".

Заметим, что "36 — сумма двух простых чисел" является финитным высказыванием. Действительно, если 36 — сумма двух простых чисел, то они обязательно меньше 36. Существует всего 11 простых чисел, меньших 36 (это 2,3,5, 7,11,13,17,19, 23, 29, 31), и 55 пар, которые из них можно образовать. Чтобы посмотреть, истинно ли высказывание, достаточно проверить одну за другой эти 55 пар и убедиться, даст ли какая-нибудь в сумме 36. Высказывание истинно, поскольку 36 = 5 + 31.

Напротив, для высказывания "43 является суммой или разностью трех последовательных простых чисел" тот факт, что мы говорим о сумме или разности, предполагает: задействованные простые числа могут быть настолько большими, насколько мы захотим. Поиск простых чисел потенциально бесконечен, поэтому высказывание не финитное.

Утверждение о том, что любое четное число является суммой двух простых, известно как гипотеза Гольдбаха. Он сформулировал ее в 1742 году в письме знаменитому швейцарскому математику Леонарду Эйлеру (1707-1783).

До сих пор неизвестно, верна ли эта гипотеза. Она выполняется для большого числа четных чисел, но до сих пор никто не нашел доказательства для всех возможных случаев, так же как и не нашли примера, при котором гипотеза была бы ложной.

Итак, если мы предложим множество аксиом арифметики, то наименьшее, чего мы можем от него требовать — это способности доказать все финитные истинные высказывания. Следует заметить: во всем, что мы только что сказали, слово "истинное" связано с финитными высказываниями. В этом ограниченном контексте "истинное" и "ложное" становятся синтаксическими условиями, поскольку они проверяются механически за конечное число шагов. С точки зрения синтаксиса программа Гильберта предполагала нахождение непротиворечивого и полного множества аксиом арифметики, которое было бы способно доказать все финитные истинные высказывания. В первой теореме Гёделя о неполноте доказывается как раз то, что эта цель недостижима.