Luis Alvarez - Самая сложная задача в мире. Ферма. Великая теорема Ферма

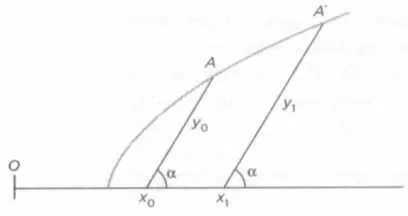
Иллюстрация метода координат Фарма и того, как определяется геометрическое место точек.

Как уже упоминалось, интерес Ферма к аналитической геометрии возник из его попыток восстановить сочинение Аполлония. В процессе этой работы он пришел к мыслям, которые отразил в своем Isagoge, где можно прочитать следующее:

"Каждый раз, когда две величины [две неизвестные) находятся в равенстве..., существует такое геометрическое место..., что конечная точка [этих величин] описывает прямую или кривую линию".

Согласно историку Карлу Бойеру, данное утверждение составляет одну из самых больших революций в истории математики. Его нельзя доказать напрямую; это постулат. Но Ферма посвящает остаток своего маленького трактата иллюстрации его пользы, анализируя частный случай кривых: конические сечения, прямую линию и окружность (которую в древности не считали коническим сечением).

Ферма не создавал прямоугольную систему координат, которая так хорошо знакома нам сегодня. Его аналитическая геометрия одноосная: определяется только ось абсцисс. Однако очевидно, что он скрыто использует ось ординат при определении расстояний.

На рисунке показаны элементы аналитической геометрии Ферма. У нас есть уравнение с двумя неизвестными x и y и константой c, ƒ(x, y) = c. Расстояние х 0— это явно значение абсциссы, в то время как ордината задана значением длины отрезка у 0. Заметьте, что угол α необязательно прямой, как это было бы в современной системе декартовых координат. На самом деле угол произволен (более поздние авторы поняли, что намного проще сделать угол α прямым). Точка, которая движется по геометрическому месту точек, — А. Мы можем видеть, как она движется к положению А' которое соответствует абсциссе х 1и ординате у 1. Следует заметить, что ƒ(x 0, у 0) - ƒ(x 1, у 1) = c, то есть уравнение выполняется для всех точек А геометрического места точек, и наоборот, точки А полностью определяются уравнением. Это ключевое соответствие между геометрией и алгеброй, предоставляемое аналитической геометрией (запись современная — Ферма не использовал запись функции ƒ(x, у)).

В этом изложении есть скрытое понятие, которое было основополагающим для развития анализа: непрерывное изменение. Используя единственную ось, Ферма сосредоточился на том, как движется точка по кривой, определяющей геометрическое место. Это концептуально отличается от процесса графического представления точек на плоскости с двумя координатными осями и помещения между ними кривой, как большинство из нас научилось делать при составлении графика. Видение Ферма динамично: оно соответствует точке, двигающейся по некоей траектории, и, следовательно, почти случайно Ферма придал физическую реальность аналитической геометрии, которая оказалась основополагающей в последующих работах Ньютона, Лейбница и семьи Бернулли. Другая отличительная характеристика системы Ферма в том, что она включает в себя только положительные величины в области и абсцисс, и ординат, поэтому его кривые всегда находятся в первой четверти плоскости и, следовательно, иногда теряется от половины до трех четвертей их протяженности. Парабола с вершиной в начале координат и фокусом на оси х, например, была бы только половиной параболы.

В приложении, которое вышло через некоторое время после Isagoge, Ферма представил общий метод превращения уравнения третьей или четвертой степени в систему уравнений второй степени. Речь идет о поиске точки пересечения между двумя кривыми. Так, уравнение х 3+ bx 2= bс с помощью введения новой переменной у превращается в два неопределенных уравнения: х 2+ bx = by, с = ху. Речь явно идет о пересечении между параболой и гиперболой. К сожалению, геометрический "дух· метода помешал Ферма найти больше одного корня (пересечения), поскольку под влиянием греков он довольствовался только одним положительным корнем. Математик пользовался этими результатами для выступления против классификации кривых Декарта в полемике, которая на сегодняшний день оказалась бесплодной, поскольку данные классификации, как выяснилось, не имеют значения.

Центральная теорема, которую Ферма доказывает в своем Isagoge, состоит в том, что все конические сечения, помимо прямой линии и окружности, могут быть выражены общими уравнениями второй степени или первой степени (в случае с прямой). Ферма делит все возможные уравнения первой или второй степени на семь "канонических" случаев, доказывая, что любое уравнение первой или второй степени можно свести к одному из них: они относятся, соответственно, к окружности, эллипсу, параболе, двум видам гиперболы и двум видам прямой линии. Доказательства для каждого случая намного более подробные, чем те, что обычно давал Ферма, но даже здесь было опущено несколько шагов, которые казались математику очевидными, поскольку они вытекали из классических сочинений, таких как "Данные" Евклида, трактат "Конические сечения" Аполлония или работа Виета.

Как и Виет, Ферма неизменно опускает синтетическое доказательство, считая его тривиальным и пользуясь только аналитическим методом, чтобы дойти от уравнения до геометрического места точек. Однако ясно: ученый считает, что его теоремы обратимы (и это соответствует действительности), то есть для любого геометрического места точек также есть уравнение. Кроме того, в своих доказательствах Ферма использовал, чрезмерно не выделяя их, ряд преобразований, типичных для аналитической геометрии, таких как перемещение круга (чтобы его центр совпадал с началом координат), вращение параболы или изменение переменной. Ученый уже знал, что он может осуществить эти преобразования, и его результат все равно не потеряет обобщенности.

Заложив основы аналитической геометрии на плоскости, Ферма затем принялся за попытки распространить свои результаты на трехмерное пространство. Однако его математические методы не справились с такой задачей. Отсутствие системы координат оказалось роковым; визуализация геометрических результатов в трех измерениях без соответствующих координат слишком сложна, и Ферма так и не добился своей цели.

Декарт был первым, кто рассуждал об алгебре как о виде мыслительного процесса, но ясно, что Ферма, менее склонный к философии, был твердым сторонником данного подхода. Им вдвоем удалось создать новое математическое мышление, актуальное и сегодня. Очевидно, что Ферма не знал этого, но, вероятно, он был одним из последних математиков, которые так глубоко интересовались классиками. Герой нашей книги хотел возродить классическую традицию, восстановив самые значимые работы, однако на самом деле похоронил ее. Инструменты, которыми он пользовался для того, чтобы раскрыть забытые секреты Древней Греции, открыли новый мир, и из-за этого многие классические греческие методы потеряли свое значение.