Мария Монтессори - Мой метод: начальное обучение

Аналогичные наблюдения повторяются и с другими квадратами, разделенными на большее количество частей. Квадратики, являющиеся четвертой частью большого квадрата (они получились в результате деления фигуры по медианам), равны между собой и равны по площади треугольникам, возникшим в результате деления большого квадрата по диагоналям. Фигуры, одинаковые по форме, но отличающиеся по размеру, являются подобными. Прямоугольник — половина большого квадрата, подобен прямоугольнику, являющемуся 1/ 8большого квадрата, при этом они не равны между собой, у них разная площадь. Также подобны друг другу большой квадрат и маленький, четвертушка большого. И т. д.

В разделении квадрата на части уже содержится идея дроби, хотя это пока еще не тот материал, который специально предназначен для изучения дробей.

Вторая серия вкладышей: дроби.

Десять дощечек с углублениями в форме круга диаметром 10 см, белого цвета. В первое углубление вложен целый круг, в остальные — такие же круги, но поделенные на 2, 3, 4, 5, 6, 7, 8, 9, 10 равных частей. Дети учатся измерять углы каждой части. Для этого мы вырезали картонный круг. Центр обозначен черной точкой на светлом фоне. Очерчен полукруг, радиус которого равен радиусу вкладышей. Этот полукруг поделен лучами на 18 секторов. Лучи выходят за пределы дуги полукруга, сверху написаны числа: 0, 10, 20 — и так до 180. Дуга каждого сектора поделена еще десятью маленькими делениями. Получилась шкала, где одно деление равно одному градусу. Линии, соединяющие 0 и 180 и идущие от центра к 90°, проведены толще, чем остальные, они чуть выпуклые, что позволяет накладывать фигуры точнее. Ученик кладет фигуру вкладыша на картонный расчерченный круг так, что вершина угла совпадает с центром, а одна из сторон заканчивается на нуле. Читаем цифру над окончанием другой стороны фигуры — это и есть величина угла в градусах. После таких упражнений, после работы с транспортиром, ребенок умеет измерять любые углы. Он знает, что круг — это 360°, полукруг — 180°, а прямой угол — 90°.

Теперь можно сосчитать, сколько градусов составляет угол седьмой части круга. 360°: 7=51°, это легко проверить наложением фигуры на расчерченный круг. Подсчеты и измерения можно повторить со всеми вкладышами, составляющими от половины до десятой части круга.

1/ 3круга = 120°, 360°: 3-120°,

1/ 4 круга = 90°, 360°: 4 = 90°, и т. д…

1/ 10 круга = 36°, 360°: 10 = 36°.

Если знаменатели равны, то сложение дробей происходит путем простого сложения числителей. Знаменатель сохраняется.

Ребенок запоминает дроби: 1/ 2, 1/ 3, ... 1/ 10У него есть и материальной восприятие, и арифметическое вычисление. С этим материалом можно совершать бесчисленные упражнения, осваивая счет с дробями. К примеру, ученик берет круг, состоящий из двух частей, и заполняет его фигурами — четвертинками круга. Он может оставить одну половину, а вместо второй положить две четвертинки. Вскоре он поймет: 1/ 2+ 1/ 2= 1/ 4+ 1/ 4+ 1/ 4+ 1/ 4, а две половинки равны четырем четвертям: 2/ 2= 4/ 4 . Ребенок мысленно считает дроби, видя части круга, и в состоянии выразить свое понимание при помощи математической записи. Наблюдения можно анализировать более глубоко.

1/ 2+ 1/ 2= 2/ 2

1/ 4+ 1/ 4+ 1/ 4+ 1/ 4= 4/ 4

1/ 2+ 1/ 2= 1/ 4+ 1/ 4+ 1/ 4+ 1/ 4

Две половины и четыре четверти — это целый круг. Заполняя круг разными по размеру частями (например, один полукруг и две четверти), ребенок видит соотношение дробных чисел.

1 = 1/ 2+ 2/ 4,то есть 1/ 2= 2/ 4. То же и с остальными дробями.

Ребенок учится сокращать дроби, видеть их простейшее выражение. Приходит очередь и сложных примеров, которые сначала выполняются при помощи вкладышей, а затем только на бумаге.

Теперь можно переходить и на другие предметы, поддающиеся счету и делению, в частности, на бусины, жетоны, фасолины.

Мы составляем приказания:

– Возьми 1/ 5от 25 бусин.

– Возьми 1/ 4от 36 жетонов.

– Возьми 1/ 3от 27 фасолин.

Бывают приказания, требующие вычислений в два действия, к тому же разными способами:

– Возьми 2/ 5от 60 бусин. 60: 5 = 12; 2x12 = 24 или 2x60 = 120;

120: 5 = 24 и т. д.

Преобразование обычных дробей в десятичные: дощечка, напоминающая круглые вкладыши, только фон не светлый, а темный, на нем обозначены деления.

Штрихи подлиннее делят круг на 10 частей, они обозначены цифрами: 0, 10… 90. Штрихи покороче делят каждую дугу пополам, еще более короткие делят каждую половину на пять частей. Получается круг, поделенный на 100 частей. Линия от центра к вершине, над которой стоит 0, (радиус) выпуклая, чтобы точнее расположить фигуры, которые мы хотим измерить.

Чтобы перевести обычную дробь в десятичную, мы берем часть вкладыша, уже измеренную, располагаем ее в нашем круге, совмещая центры и одну из сторон фигуры с выпуклым радиусом. Остальная часть фигуры должна лежать справа от радиуса, в сторону увеличения цифр. Если мы положим так одну четвертую часть круга, то сразу увидим по цифре над окончанием второй стороны фигуры, что 1/ 4 — 0, 25.

Можно положить рядом, сторона к стороне, несколько фигур-вкладышей и увидеть:

1/ 3+ 1/ 4+ 1/ 8 =0,70 (примерно).

Этот материал прекрасно развивает арифметические навыки. Круг (единичное целое) поделен на 100 частей, и мы можем делить эти 100 фрагментов на любое количество долей. Все, что получится, будет сотыми частями целого. 1/ 4= 100: 4 = 25 сотых, то есть 25/ 100 или 0,25. Деление совершается делением числителя на знаменатель: 1:4 = 0,25.

Третья серия вкладышей: равные по площади фигуры.

Этот материал позволяет вычислять площади разных фигур и дает предварительное представление о некоторых геометрических теоремах, которые обычно не изучаются в начальной школе. Считается, что это недоступно пониманию маленьких детей.

Треугольник и прямоугольник равны по площади, если одна сторона прямоугольника равна основанию треугольника, а другая сторона прямоугольника равна половине высоты треугольника.

На широкой прямоугольной рамке есть два белых пространства (две выемки): равные по площади треугольник и прямоугольник.

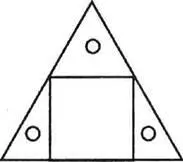
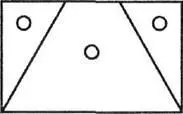
Вкладыши составлены так, что могут заполнить и прямоугольное, и треугольное пространство. Это треугольник, состоящий из трех частей.

Параллельная линия делит высоту треугольника пополам, вертикальная делит верхнюю часть на два равных треугольника. Можно наложить эти маленькие верхние треугольнички друг на друга и убедиться, что они равны.

Работа с бусинами и числовым квадратом научила детей находить площадь квадрата, умножая одну сторону на другую. Площадь прямоугольника также равна произведению смежных сторон. Работая с вкладышами, ребенок видит, что треугольник превращается в прямоугольник. Значит, их площади равны. Следовательно, площадь треугольника равна произведению его основания на половину высоты.