Роберт Фрэнк - Успех и удача [Фактор везения и миф меритократии] [litres]

Для данного простого распределения средний уровень квалификации составляет 50:

По мере умножения числа участников состязания мы видим расширение диапазона уровней их квалификации. Иначе говоря, чем больше игроков, тем шире разброс их мастерства и, следовательно, тем выше максимальный уровень квалификации среди участников:

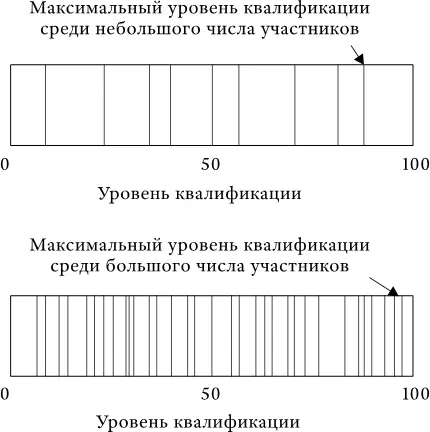
Если провести тысячу соревнований, каждое с участием лишь двух соперников, то средний уровень квалификации лучшего из двух игроков составит 66,7. Средний уровень квалификации худшего из двух игроков составит 33,3.

Аналогичным образом средний уровень квалификации лучшего из трех участников составит 75:

А средний уровень квалификации лучшего из четырех участников составит 80:

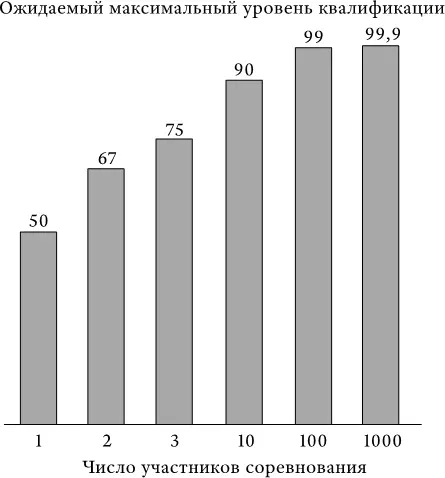
В общем, среднее значение максимального уровня квалификации наблюдаемого в состязании N-го количества участников будет равно: 100 [N/(N + 1)]:

В этом примере ожидаемый максимальный уровень квалификации с увеличением числа участников неуклонно растет, но по мере этого увеличения каждый прирост уровня квалификации становится все меньше и меньше.

Добавим в эту картину фактор удачи. Как и прежде, уровень квалификации каждого участника – это случайное число, с равной вероятностью принимающее любое значение от 0 до 100. Однако на этот раз эффективность зависит не только от квалификации, но и от удачи, также являющейся случайным числом, с равной вероятностью принимающим любое значение от 0 до 100. Чтобы отобразить сравнительную значимость квалификации и удачи, я допускаю, что эффективность каждого участника представляет собой взвешенную сумму значений квалификации и удачи, где подавляющая часть веса придается квалификации, и лишь небольшая часть – удаче. Например, если предположить, что эффективность зависит на 95 % от квалификации и лишь на 5 % – от удачи, то игрок с уровнем квалификации, равным 90, и уровнем удачи, равным 60, будет иметь уровень эффективности: 0,95 × 90 + 0,05 × 60 = 88,5, что лишь немного ниже уровня квалификации такого участника.

Поскольку удача – это, по определению, величина случайная, то наиболее естественным будет предположить, что корреляция между удачей и квалификацией отсутствует. Таким образом, самый квалифицированный участник имеет не больше шансов оказаться удачливым, чем любой другой. Например, самый квалифицированный из 1000 участников будет иметь ожидаемый уровень квалификации, равный 99,9, но ожидаемый уровень удачи – лишь 50.

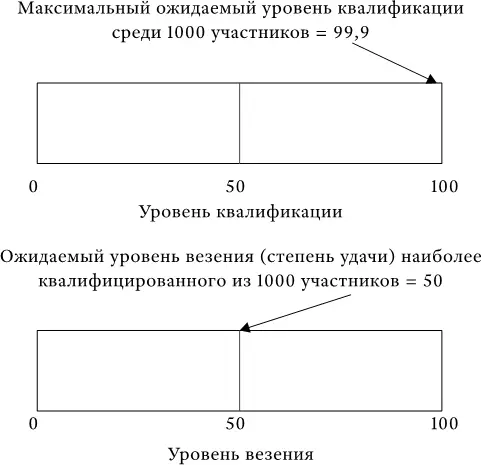
Следовательно, ожидаемый уровень эффективности наиболее квалифицированного из 1000 участников: P = 0,95 × 99,9 + 0,05 × 50 = 97,4, что лишь на 2,6 пункта ниже максимального значения. Однако при наличии 999 соперников такой уровень эффективности для победы данного участника оказывается в обычных условиях недостаточным.

При наличии 1000 участников ожидается, что 10 из них покажут уровень квалификации, равный 99 или выше. Среди этих 10 наивысший ожидаемый уровень везения (удачи) составит: (10/11) × 100 = 90,9. Таким образом, наивысшая ожидаемая оценка эффективности среди 1000 участников должна быть не ниже: P = 0,95 × 99 + 0,05 × 90,9 = = 98,6, что на 1,2 пункта выше ожидаемой оценки эффективности наиболее квалифицированного участника.

Короче говоря, среди 1000 участников почти всегда найдется тот, кто почти так же талантлив, как и наиболее талантливый участник, но при этом значительно его удачливей. Вывод таков: даже если удача обеспечивает лишь малую долю общей эффективности, победитель в крупном соревновании редко будет самым квалифицированным участником, но, как правило, окажется одним из наиболее удачливых.

На следующих рисунках представлены результаты дополнительного моделирования, где эффективность зависит от трех факторов: способности, усилия и удачи. В этих примерах усилие и способность учитываются одинаково и вместе составляют львиную долю общей эффективности любого участника. Доля удачи в эффективности в разных случаях варьируется в весовом диапазоне от 1 до 20 %. Для каждой комбинации весов я также допускаю, что число участников может варьироваться от 1000 до 100 тыс. Количество участников в каждом моделировании составляет 1000. Все оценки способности, усилия и удачи – это реальные цифры, которые с равной вероятностью принимают любое значение от 0 до 100.

На рис. П 1.1 представлены средние оценки фактора везения у победителя (для этих случаев моделирования), а на рис. П 1.2 – процент победителей, не обладавших наивысшей оценкой «способности + усилия» среди всех участников.

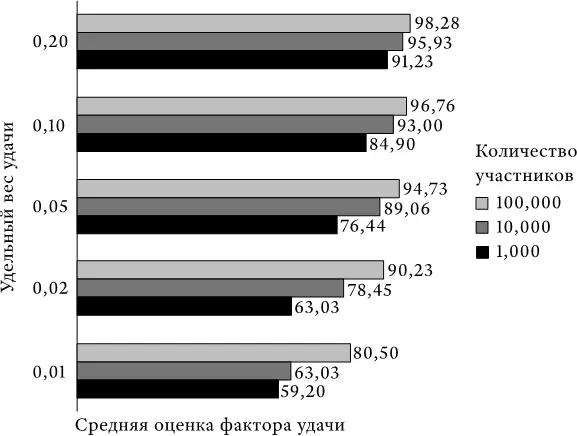
Рис. П 1.1. Средняя оценка фактора везения (удачи) у победителя

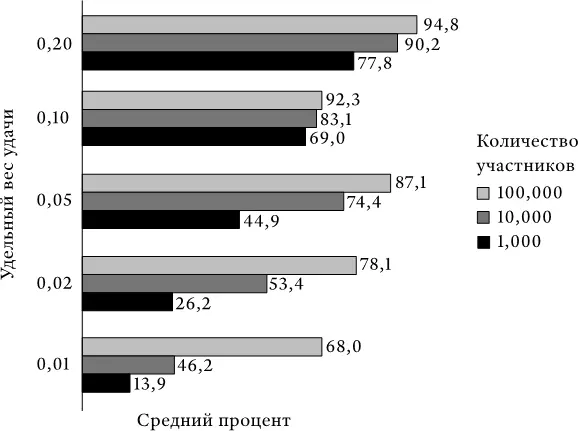
Рис. П 1.2. Процент победителей, не обладавших наивысшей оценкой «способности + усилия»

Чем прогрессивный налог на потребление отличается от других потребительских налогов, таких как налог с продаж и налог на добавленную стоимость?

Налог на добавленную стоимость (НДС) аналогичен обычным налогам с продаж, взимаемым в большинстве штатов. Недавние предложения о принятии налога, взимаемого по единой ставке (flat tax), подразумевают замену действующего подоходного налога (для юридических лиц – налога на прибыль) национальным налогом с продаж. В случае налогов с продаж, которые обычно взимаются при расчете (на кассе), покупатели платят фиксированный процент от доналоговой отпускной цены приобретаемого товара. Налог на добавленную стоимость, как следует из его названия, представляет собой налог, взимаемый с каждого повышения цены изделия на каждом этапе его обработки в процессе производства. Функционально налоги на добавленную стоимость в основном эквивалентны стандартным налогам с продаж (т. е. с оборота). В итоге покупатели каждый раз платят налог в виде фиксированного процента от цены приобретаемого товара.