Ричард Нисбетт - Что такое интеллект и как его развивать. Роль образования и традиций

Любые явления можно схематически изобразить в виде кривой нормального распределения, изображенной на рисунке А1, имеющей колоколообразную форму. Например, если нам нужно представить в виде графика количество яиц, откладываемых ежедневно разными курами, число ошибок, возникающих при производстве разных типов автомобилей, или результаты IQ-тестов для группы людей, форма графика, представляющего эти данные, будет приближаться к колоколообразной. Нам нет надобности углубляться в математические обоснования того, почему графики распределения имеют такую форму. Важно то, что график нормального распределения помогает строить предположения о том, где будут находиться данные наблюдения относительно других данных. График нормального распределения на рисунке А1 разделен на области стандартных отклонений, называемых так потому, что норма представляет собой отклонение от среднего значения (примерно) на эту величину. При абсолютно нормальном распределении, которое является математической абстракцией, однако встречается достаточно часто при очень большом количестве данных, примерно 68% всех данных наблюдений попадают в область от +1 до -1 стандартного отклонения (СО) от среднего значения (которое на рис. А1 представлено нулевой точкой).

Кроме того, в концепции стандартного отклонения для нас полезно то, что касается отношений между процентильными значениями и стандартным отклонением. Примерно 84% всех наблюдений попадают в область значений, которые на 1 СО или менее выше среднего; наблюдения выше среднего ровно на одну величину СО находятся на 84-й процентили распределения. Оставшиеся 16% находятся за пределами одной величины стандартного отклонения. Почти 98% всех наблюдений попадают в область, равную или превосходящую среднее значение на 2 СО. Результат, превышающий среднее ровно на 2 СО, находится на 98-й процентили. Оставшиеся 2% результатов лежат выше. Практически все результаты наблюдений попадают в рамки от -3 до +3 СО. По договоренности СО в распределении результатов IQ-тестов принято считать равным 15 (при среднем значении, равном 100).

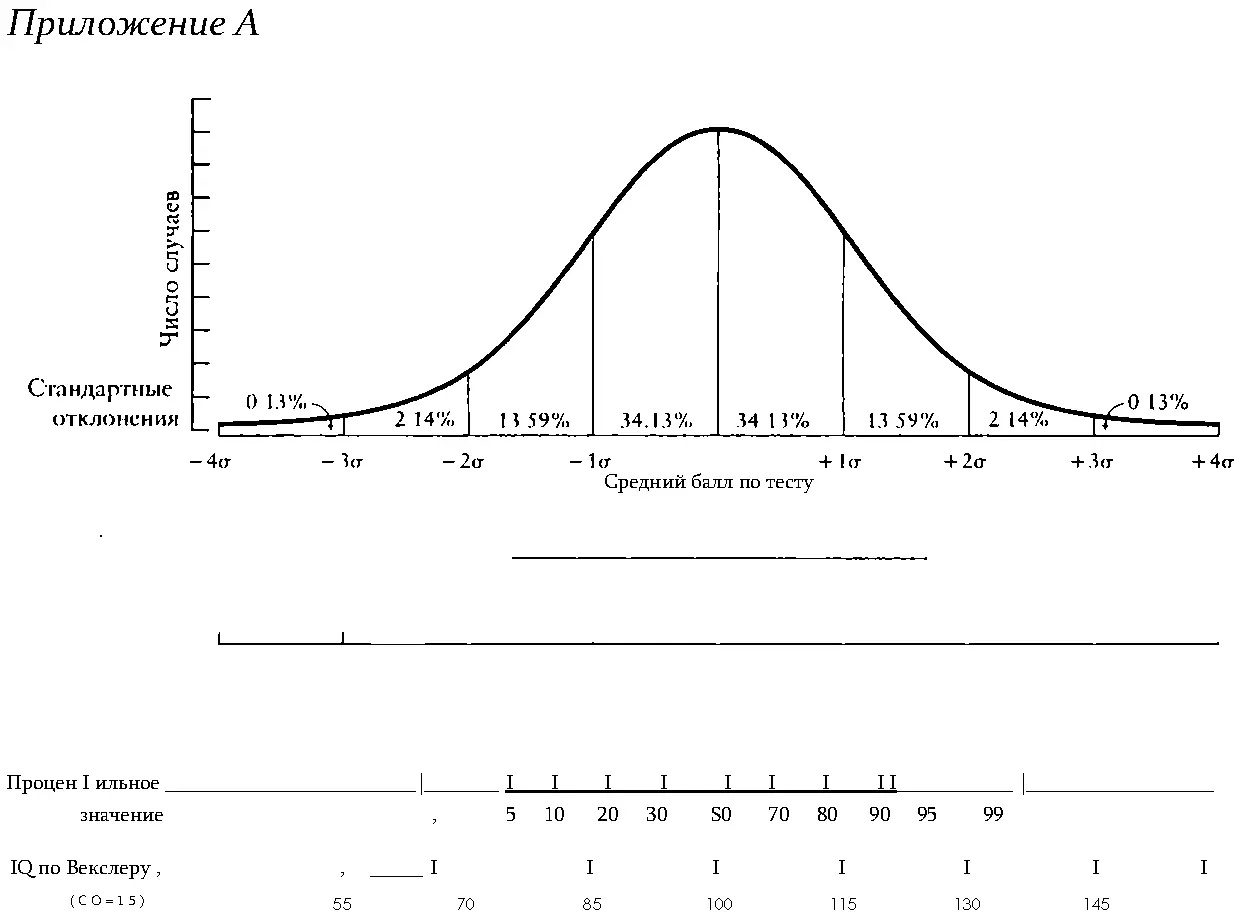
Рис. А1. Кривая нормального распределения, где стандартные отклонения от среднего отмечены вертикальными линиями, с соответствующими процентильными значениями и результатами IQ-теста Векслера, приведенными внизу. Обратите внимание, что 68% результатов попадают в область от -1 до +1 стандартного отклонения (σ) от среднего.

Стандартными отклонениями удобно пользоваться при описании размера эффекта, например, если нужно выяснить, какое влияние на знания учеников оказывает новая методика преподавания. Наиболее часто используемый в статистике индикатор размера эффекта — это так называемый параметр Коэна d, который рассчитывается следующим образом: из среднего значения для группы А вычитается среднее значение для группы В, и разность делится на среднее из стандартных отклонений двух групп (или иногда только на СО для группы А).

Параметр d меньше или равный 0,20 принято считать малым. Это значение эквивалентно изменению показателей экспериментальной группы с 50-й до 60-й процентили. Возможно, такое изменение не покажется вам слишком маленьким, если речь идет о том, чему может научиться ваш ребенок при новой методике (60-я процентиль) по сравнению со старой (50-я процентиль). А захотите ли вы платить за эту новую методику, зависит от того, насколько существенна разница между 50-й и 60-й процентилью. Если при измерении эффективности метода речь идет, к примеру, о том, насколько быстро ребенок научится печатать со скоростью 40 слов в минуту, и разница между 50-й и 60-й процентилью составляет несколько дней, вероятно, вы не захотите платить за это слишком много, равно как и не захотите взваливать эти расходы на систему школьного образования. Если же вы сравниваете эффективность двух методик преподавания математики в старших классах, используя средние показатели по тесту SAT, и одна методика дает средний балл в 500, а другая — в 520, эта разница также будет соответствовать разнице между 50-й и 60-й процентилью (принимая стандартное отклонения в результатах SAT за 100). Наверное, вы будете готовы заплатить за это какое-то количество денег, возможно, даже немалое. И, вероятно, будете довольны, если ваш школьный совет решит потратить небольшую сумму в расчете на каждого ученика, чтобы обеспечить преподавание по более эффективной методике.

Параметр d, равный 0,50 или около того, считается средним. Однако в сфере тестов на IQ и академической успеваемости такой размер эффекта считается просто бомбой! В показателях SAT по математике это разница между результатом в 500 баллов, которого может быть достаточно для поступления в неплохой университет, и в 550 баллов, который может гарантировать поступление в один из лучших университетов. Вы и ваша школа должны быть готовы заплатить немаленькую сумму за внедрение новой методики, которая могла бы поднять результат среднестатистического ребенка с 50-й на 70-ю процентиль (что соответствует разнице в 0,50 СО).

Размер эффекта от 0,70 до 1,00 СО считается большим. Для образования и различий в интеллектуальных способностях целая величина СО — это очень много. Предполагается, что различие в IQ между черными и белыми составляет как раз порядка 1,00 СО. В главе 6 мы уже обсуждали, можно ли считать этот показатель реальной разницей. Если так, то это означает, что средний показатель IQ у чернокожих находится на 16-й процентили распределения показателей IQ у белых. Если какая-либо программа школьного вмешательства позволяет улучшить успеваемость детей по математике с уровня, приблизительно равного 50-й процентили в распределении показателей по стране, до 84-й, ее внедрение целесообразно даже при высоких затратах. Для всей нации в целом повышение конкурентоспособности, к которому может привести такое улучшение показателей, должно дать очень большой экономический эффект.

Коэффициент корреляции — это показатель степени линейной зависимости между двумя переменными. Например, корреляция между показателями IQ и школьными оценками составляет примерно 0,50, то есть зависимость между ними довольно высока. В данном случае стоит ожидать хотя бы средней степени зависимости, так как IQ-тесты были изобретены для того, чтобы предсказывать возможные школьные успехи детей. Коэффициент корреляции может составлять от -1 (полная отрицательная зависимость) до +1 (полная положительная зависимость). Коэффициент корреляции, равный 0, отражает отсутствие всякой связи. Коэффициент корреляции — это еще один способ измерения размера эффекта или, скорее, степени отношения между показателями, где значения ниже 0,30 считаются несущественными, от 0,30 до 0,50 — средними, а выше 0,50 — высокими. Но так же, как и в случае с размером эффекта, важность корреляции оценивается в большей степени не по ее величине, а по переменным, которые рассматриваются в данном случае. Коэффициент корреляции можно перевести и в термины стандартного отклонения. Корреляция между двумя переменными, равная 0,25, означает, что повышение одной переменной на 1 СО приводит к повышению второй на 0,25 СО; корреляция, равная 0,50, — повышение на 0,50 СО. Следовательно, если корреляция между размером класса и показателями успеваемости по стандартизированным тестам составляет -0,25, значит, уменьшение класса на 1 СО должно приводить к улучшению оценок на 0,25 СО (если считать, что между размером класса и успеваемостью действительно существует причинно-следственная связь).