Теоретические основы телепатии
- Название:Теоретические основы телепатии
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Теоретические основы телепатии краткое содержание
Теоретические основы телепатии - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В соответствии с рисунком эксперимент разобьем на три независимые части. Вначале организуем передачу таким образом, чтобы исключить в качестве параметров, несущих информацию – форму и размер, а оставим только цвет. С этой целью возьмем два круга равного диаметра и из одного материала, например, бумаги, окрашенные в зеленый и оранжевый цвета – Рис. 5.3.
размер
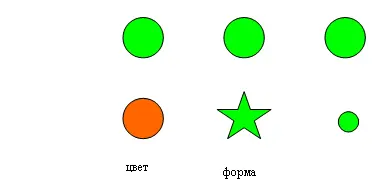
Рис. 5.3. Множество сигналов для передачи
Здесь необходимо подчеркнуть, что условия проведения всех экспериментов, очевидно, должны быть одинаковыми, поэтому в качестве исходной информации используем одну и ту же случайную последовательность нулей и единиц: 1 1 0 1 0 0 0 1 1 0, которые в каждом из опытов будем заменять соответствующими картинками. В качестве первого шага, подготовим для индуктора к передаче последовательность, составленную из кругов зеленого – З и оранжевого – О цвета, Табл. 5.2. Таким образом, создадим условия для реализации первого слагаемого (5.1) – L [ 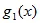 ].
].
Таблица 5.2
К передаче цвета изображения
| Передано | О О З О З З З О О З |
| Прием 1 | О О З О З З З О О З |
| Прием 2 | О О З О З З З О О З |
| Прием 3 | О О З О З З З О З З |
Далее действие развивается по знакомому сценарию – перципиент, глядя поочередно, на зеленый или оранжевый круг – 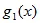 , выбирает тот из них, которому в то же самое время, по его ощущениям, соответствует сигнал от индуктора
, выбирает тот из них, которому в то же самое время, по его ощущениям, соответствует сигнал от индуктора 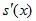 . После идентификации последней из тридцати картинок нетрудно вычислить вероятность правильного приема для каждого цвета:
. После идентификации последней из тридцати картинок нетрудно вычислить вероятность правильного приема для каждого цвета:
р(З)= 15/15=1.0 – вероятность приема зеленого круга и р(О)= 14/15=0.93 – вероятность приема оранжевого круга, а также вероятность одного символа, безразлично какого, р = 29/30 = 0.967 .
Результаты говорят сами за себя – перципиент оценивает принятый от индуктора цвет изображения с вероятностью, свидетельствующей об отсутствии каких либо искажений. Другими словами, сознание человека относительно данного параметра представляет собой линейную систему.
Во втором опыте в качестве переносчика информации оставим одну лишь форму изображения, соответственно, исключив – цвет и размер. Для реализации этого плана используем небольшой зеленый круг и зеленую же пятиконечную звезду – Рис. 5.3, причем их площади сделаем одинаковыми. Результаты опыта отражены в Табл. 5.3, где обозначено: К – круг зеленого цвета, З – звезда, тоже зеленого цвета. Тем самым создадим условия для реализации второго слагаемого (5.1) – L [ 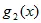 ].
].
Таблица 5.3
К передаче формы изображения
| Передано | З З К З К К К З З К |
| Прием 1 | З З К З К К К З З К |
| Прием 2 | З З К З К К З З К К |
| Прием 3 | З З К К З К К З К К |
После приема и идентификации всех символов, найдем вероятности правильного приема для каждой из фигур в отдельности, а именно: р(К)= 13/15=0.867 – вероятность приема круга, р(З)= 12/15=0.8 – вероятность приема звезды. Соответственно, для вероятности одного символа, круга или звезды, получим, р = 25/30 = 0.833 . Итак, использование в качестве информационного параметра формы передаваемой картинки дает вполне приемлемый результат, который может быть существенно улучшен в дальнейшем с помощью одного из методов защиты от ошибок. Таким образом, в случае обработки информации исключительно по форме изображения, сознание также ведет себя как линейная система.
Наконец, перейдем к третьему эксперименту, в соответствии с которым будем передавать круги одинакового зеленого цвета – Рис. 5.3, имеющие диаметры 6 и 14 см. То есть, в качестве информационного параметра здесь используем только размер (или площадь) картинки, остальные – такие как цвет и форма, будут совпадать. Результаты опыта отражены в Табл. 5.4, где обозначено: Б – большой круг, М – малый круг. Здесь созданы условия для реализации третьего, последнего слагаемого (5.1) – L [ 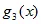 ].
].
Таблица 5.4
К передаче размера изображения
| Передано | М М Б М Б Б Б М М Б |
| Прием 1 | М М Б Б Б Б Б М М Б |
| Прием 2 | М М Б М Б Б Б Б М Б |
| Прием 3 | М Б Б М Б Б Б М М М |
Вероятности правильного приема для каждого изображения будут: Р(Б) = 14/15 = 0.933 – вероятность для большого круга, Р(М) = 12/15 = 0.8 – вероятность для малого круга. Соответственно, для одной картинки, безразлично какой, большой или малой, получим: р = 26/30 = 0.867. Если теперь сравнить этот результат с двумя предыдущими, когда в качестве параметров использовались только цвет и только форма, то можно придти к аналогичным выводам.
Итак, три независимых эксперимента, выполненные с одними и теми же исходными последовательностями и в одних и тех же условиях, показали вероятности правильного приема одного символа, близкие к единице. Таким образом, можно констатировать, что в системе мысленной передачи индуктор-перципиент искажения информации практически отсутствуют, что свидетельствует о линейности сознания как индуктора, так и перципиента [46]. Руководствуясь результатами опытов, имеем:
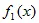 =
= 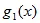 *
* 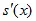 ,
,
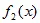 =
= 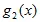 *
* 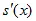 , (5.3)
, (5.3)
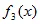 =
= 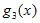 *
* 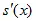 .
.
Подставляя эти равенства в (5.1) и учитывая свойство дистрибутивности свертки, можно записать:
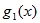 *
* 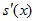 +
+ 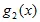 *
* 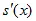 +
+ 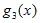 *
*  =
=  *[
*[ 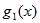 +
+ 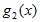 +
+  ]. (5.4)
]. (5.4)
и, так как
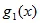 +
+ 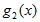 +
+ 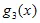 = s(x) , (5.5)
= s(x) , (5.5)
то
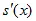 * s(x) = f(x) (5.6)
* s(x) = f(x) (5.6)
Интервал:
Закладка: