Аркадий Егидес - Лабиринты мышления или учеными не рождаются

Здесь остановимся на таком аспекте проблемы. Классификация предполагает родовидовое деление в сторону конкретизации и в сторону обобщения. Род «легковой автомобиль» делится на виды по маркам (конкретизация). В то же время понятие «легковой автомобиль» объединяется с понятием «грузовой автомобиль» в понятие «автомобиль» (обобщение). В этом обобщении родовым понятием выступает понятие «автомобиль». А понятия «легковой автомобиль» и «грузовой автомобиль» — видовые. При таком понимании соотношение понятий как бы унифицируется и всегда выступает как родовидовое (видо–родо–вое). И любому старшекласснику легко понять, что в классификации Карла Линнея «тип» относится к «классу», «класс» относится к «роду», «вид* относится к «отряду», «отряд» к «подотряду» — как «род» относится к «виду». Возражений по поводу удобства терминологии Линнея нет, но следует понимать и то, что мы сейчас обсудили.

Выражение «в жанре науки»мы впервые услышали из уст профессора–психолога А. Ф. Ануфриева, и оно нам пришлось по душе. А поскольку мы его будем и дальше использовать, то неформальным «спасибо» здесь и почтим авторство Александра Федоровича.

В науке нет единой условной системы. Поэтому разные авторы и говорят то о классификации, тоо типологии.Но и под классификацией, и под типологией обычно понимается разветвленное деление по родовидовому принципу (если использовать термины, предпочитаемые в логике). В классификации Линнея «род» и «вид» находятся в середине классификационной линии. Тем не менее говорят не о «ро–дофикации», а о классификации. Вряд ли стоит менять привычку, но применять ее стоит с дополнительными пояснениями. И стоит помнить о перекрестах. Это тоже относится к классификации.

Родовидовое соотношение

и проблема определения понятий

В любой науке много усилий тратится на определения. Если говорить латинизированными терминами — на дефиниции. И слово «определение», и слово «дефиниция» можно понимать как установление пределов. Определение — это «о–предел–ение». Можно употребить синоним: «о–граничение». Корень «-фин-» в латинских словах означает конец (отсюда финиш, финал). Так что дефиниция может быть переведена как «о–конечивание».

В логике говорят об объеме и содержании понятия.

Мы ставим некоторые пределы, границы, «концы» в том, что входит в данное понятие. Например, в понятие «прямоугольный треугольник» входят египетский треугольник (у него соотношение сторон, как помним: 3–4—5) и прямоугольный треугольник с иным соотношением сторон. В него могут войти прямоугольные треугольники маленькие и большие. Вот как раз перечисление того, что входит в понятие —это его объем.Асодержаниепонятия — втом, какими призна–ками описываются его пределы, границы. Сказанное сейчас — не более чем пересказ фрагмента соответствующего раздела в логике. Но в деле определений в науках царит некоторым образом хаос.

Разные авторы понимают под определением часто очень разные вещи. Некоторые из ученых мужей полагают, что они дали определение, а на самом деле предложили лишь тавтологию. Типа: треугольник — это то, что имеет три угла К этому виду можно отнести и просто перевод с языка на язык. Вот, например: дефиниция — это определение.

Часто все сводится к описанию составных частей. Гидросфера Земли — это реки, озера, моря и океаны, пар и облака.

Или перечисляется то, что составляет объем понятия. Четырехугольники — это прямоугольники, квадраты, ромбы, трапеции.

И наконец, определяемое понятие (видовое) подводится под более общее понятие (родовое), и описываются признаки, отличающие определяемый вид от других видов данного рода. Большая часть ученых, не сговариваясь, понимают под определением именно этот вариант. Примем его и мы. И тогда в соответствии с этим примем и то, что родовидовое соотношениепонятий лежит в основе и определений.

Так понимаемое определение и то, что мы имеем в виду, когда говорим о классификации — две стороны одного и того же мыслительного процесса. Итам, и там происходит уяснение соотношения понятий. Нередко в речи преподавателя или в тексте книги специально говорится о классификациии специально даются определения.Но нередко они только подразумеваются. Преподавателям, студентам и ученикам (а авторам монографий тем более) имеет смысл всегда, а не иногдапрояснять ситуацию. И логико–графическое структурирование помогает высветлить опоры для определений в соответствии с той или иной классификацией.

Выше, на рис. 112, мы привели классификацию рыб. Эта логико–графическая схема читателю уже, наверное, запомнилась, так что не будем здесь ее повторять. А сразу с учетом ее дадим определение (см. рис. 117).

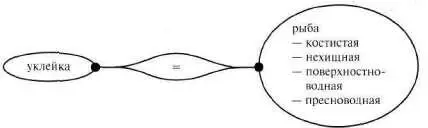
Рис, 117

Договоримся, что определения так и будем давать. В одной фигуре — «определяемое» (уклейка). В другой — «определяющие» слова. Между ними в расширении связующей линии с жирными точками по концам — знак равенства. В сущности, и там, и там одно и то же понятие, только обозначенное разными словами. Но… все это будит и дисциплинирует мысль. Встает, например, вопрос: а почему, собственно, уклейка — это рыба, а не позвоночное или даже не хордовое… И медведь — почему это хищное млекопитающее, а не обитатель леса… То есть если совсем системно, то уж тогда все перечисляем, а не–толь–ко то, что хаотично и случайно выхвачено нашим фрагментарным мы–шлением… И, по крайней мере, будем осознавать эту хаотичность, которая нам мила сию секунду, но является только отправной точкой…

В научных текстах и схемах имеет смысл подчеркивать связь определений и классификаций.Излагая классификацию, туг же давать определения входящим в нее понятиям. Треугольники делятся на прямоугольные, тупоугольные, остроугольные. Каждый из них может быть равнобедренным и неравнобедренным… До сих пор мы излагали классификацию.А теперь дадим определение, вписанное в эту классификацию. Треугольник с соотношением сторон 3—4–5 (называемый египетским) — это неравнобедренный прямоугольный треугольник.

Тогда и встанет вопрос о том, какдавать определение медведю: как млекопитающему, как хищнику, а может бьпь, как обитателю леса… А то и как цирковому животному… То есть мы берем понятие из классификационной системы, придаем ему статус видового понятия и описываем те или иные признаки, отличающие его от других видов такого–то рода. Понимаем при этом всю условность и неполноту нашего толкования понятийных соотношений… Но вот мы почему–то начинаем более полно и более точно представлять в уме эти соотношения, и это развивает наши знания… Так что вряд ли имеет смысл отказываться от таких рассуждений… Только бы это не оказалось бесплодным бесконечным мудрствованием…