Аркадий Егидес - Лабиринты мышления или учеными не рождаются
- Название:Лабиринты мышления или учеными не рождаются
- Автор:
- Жанр:
- Издательство:АСТ-Пресс Книга
- Год:2004
- ISBN:5-462-00109-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Аркадий Егидес - Лабиринты мышления или учеными не рождаются краткое содержание
Лабиринты мышления или учеными не рождаются - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
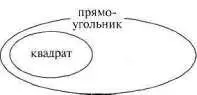
Рис. 91
Прямоугольник — это вид параллелограмма (см. рис. 92).

Рис. 92
Ромб — это вид параллелограмма (см. рис. 93).
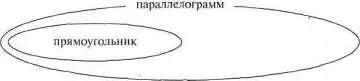
Рис. 93
Ромб и прямоугольник — понятия перекрещивающиеся (см. рис. 94).
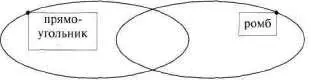
Рис. 94
Квадрат — это вид прямоугольника с равными сторонами. И одновременно квадрат — это вид ромба. Ведь квадрат — это ромб с прямыми углами. Поэтому квадрат помещаем в перекрестье прямоугольника и ромба. При этом понятие «квадрат» берем в отдельный овал. Здесь, как видим, из трех простых схем мы делаем одну сложную, в которой показано соотношение понятий «ромб», «прямоугольник», «квадрат» (см. рис. 95).
Рис. 95
Теперь включаем в эту сложную схему понятие «параллелограмм».' Поскольку ромб и прямоугольник — виды параллелограмма, то всю уже достаточно сложную схему заключаем в овал, означающий фигуру–понятие «параллелограмм». И получаем еще более сложную схему (см. рис. 96).
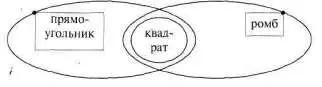
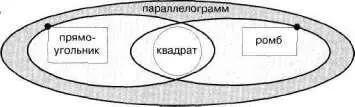
Рис. 96
Понятно, что все это четырехугольники. Так что заключаем их в общую рамку (см. рис. 97).
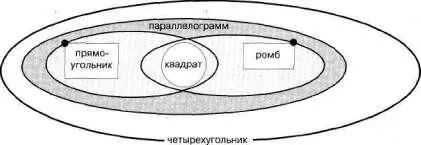
Рис. 97
Между прочим, то, что прямоугольник и ромб — виды параллелограмма, звучит не так уж странно. А вот квадрат параллелограммом обычно не называют. Тем не менее это так. И это видно на схеме.
А есть еще трапеция. Она четырехугольник, но ведь не параллелограмм же. Ее, ладно, поместим в рамке «четырехугольник», но рядо–положно с рамкой «параллелограмм» (см. рис. 98).
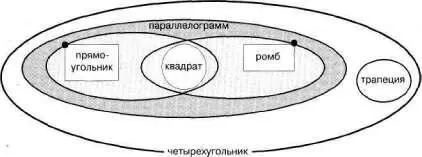
Рис. 98
Но ведь могут быть и четырехугольники, которые нельзя назвать ни трапециями, ни параллелограммами. Стороны у такого четырехугольника не равны и не параллельны, но углов четыре. Изображения таких четырехугольников представлены на рис. 99.
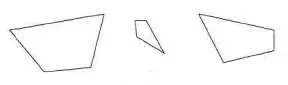

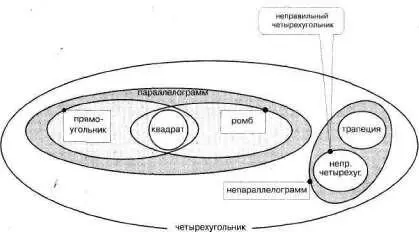
Рис. 100
То, что представлено наглядно на приведенной схеме, можно выразить многословным текстом. Четырехугольники делятся на па–раллелограммы и непараллелограммы. Непараллелограммы делятся на трапеции и четырехугольники неправильной формы. Параллелограммы могут быть прямоугольниками и могут быть ромбами. Прямоугольник может быть квадратом. Некоторые ромбы являются одновременно прямоугольниками. Тогда это квадраты. Квадрат — это и ромб, и прямоугольник, и конечно же параллелограмм. Ромб может быть прямоугольником, тогда это квадрат. Непараллелограмм не может быть ромбом или прямоугольником. Конечно же он не может быть и квадратом. И так далее. Но в тексте нет той наглядности, которая делает материал легко понимаемым и легко запоминаемым.
Вернемся к рис. 84 и рис. 87.
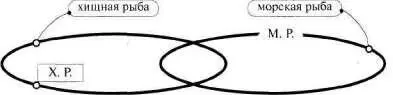
Рис. 84

Рис.Й7
На каждом из них представлен простой (одинарный) перекрест. То есть перекрест двух понятий. А на рис. 50 перекрещиваются несколько понятий. Также, как на рис. 100. В этих случаях мы имеем дело со сложными понятийными перекрестами.
При этом в рис. 50 на хэтчбэки и седаны делятся только легковые автомобили. А в рис. 100 делятся на трапеции и неправильные четырехугольники только «непараллелограммы». А параллелограммы охватывают перекрещивающиеся понятия «прямоугольник» и «ромб». Ну что ж, учтем, что может быть и так.
Но возможен и другой, как бы более «логичный» вариант.
Вернемся к «рыбам». Тот перекрест понятий «хищная рыба» и «морская рыба», который мы видим на рис. 84, не единственно возможный, если говорить о классификации рыб в целом. «Перекрестим» понятия «хищная рыба» и «пресноводная рыба» (см. рис. 101).
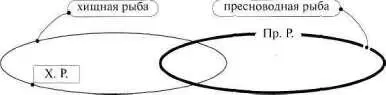
Рис. 10]
А теперь «перекрестим» понятия «нехищная рыба» и «пресновод-•ная рыба» (см. рис. 102).

Рис. 102
Ну и теперь — уж никуда не денешься — «перекрестим» «нехищную рыбу» и «морскую рыбу» (см. рис. 103).

Рис. 103
Атеперь… Теперь тоже никуда не денешься, произведем такую атаку на проблему — поместим каждую из этих простых схем в единое пространство (см. рис. 104).

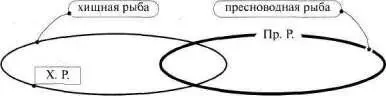
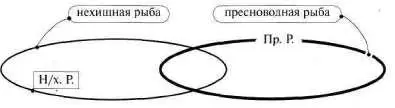

Рис. 104
Взаимное расположение фигур–понятий несколько видоизменим. Пусть читатель внимательно проследит за этими изменениями.
Аббревиатуры читатель, наверное, запомнил, так что далее мы не будем повторять выноски (см. рис. 105).
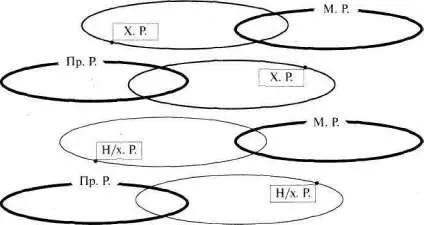
Рис. 105
Теперь преобразуем всю картину так: фигуры с одинаковыми понятиями обведем едиными рамками (см. рис. 106).
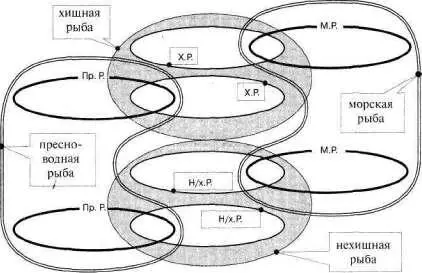
Интервал:
Закладка:








