Аркадий Егидес - Лабиринты мышления или учеными не рождаются

ные связи. А для других соотношений, если они с нашей позиции достойны логико–графического структурирования, можно применить всеобщий способ.

Выделяем в рамках главные понятия и обозначаем характер их соотношений текстом или условными символами в расширении связующей линии (см. рис. 140).

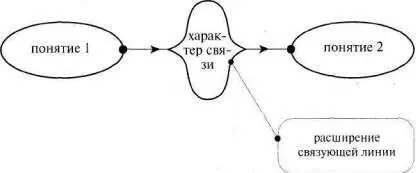
Рис. 140

Приведем пример того, как может быть использована эта структура для выражения мысли (см. рис. 141).

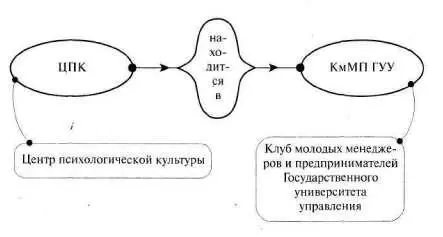
Рис. 141

Если вы обратили внимание на стрелки до и после расширения связующей линии, то предупредим: они не указывают на причинно–следственную связь, а лишь показывают направление мысли от одно–то понятия к другому. Сначала говорится: «центр психологической культуры». Потом говорится, что он «находится в…». Потом: «Клуб молодых менеджеров и предпринимателей Государственного университета управления». Подчеркнем, что направление мысли и текстуальные вставки дают недостаточно жесткое представление о соотношении понятий, но догадаться об этом соотношении очень легко. Так что такая свобода вполне приемлема.

При такой «свободной» форме логико–графического структурирования увеличивается роль текстуальных вставок. Но чтобы текст не очень мешал воспринимать соотношения фигур–понятий, можно позаимствовать из разных наук применяемые в них условные символы. Больше (>), меныпе(< ), равно (=), сумма (Ј)…. Кому что известно и приемлемо, тот то и может использовать. С одним важным условием. Если этот материал не для личного пользования, а для передачи мысли другим,то обо всех условных обозначениях надо договориться заранее. Иубедиться, что эти обозначения понятны другим. Например, есть значок «принадлежность»: е . Но он многим неизвестен. Поясните его (в выноске), сошлитесь на источник. Однако даже если вы сами автор условного символа или сокращения, то надо еще не забыть, что он означает. Расшифруйте его в доступном месте листа (экрана, доски).

* * *

Читатель, наверное, обратил внимание, что мы стараемся давать примеры из очень разных областей знания. Этим мы вместе приучаемся к мысли, что предлагаемая технология на самом деле пригодна для самых разных научных тем. Бьп — это тоже сфера информации, так что и в быту приемлемы наши стрелки и кружочки. Логико–графическое структурирование на бытовые темы — тренировка в переходе к собственно научному логико–графическому структурированию. Ну а с другой стороны, чтобы на сосредоточенном лице появилась тень улыбки, сообщим, что щенок Пушок родился после Второй мировой войны. От истины мы здесь ни на шаг, а все же не так угрюмо. Но никуда не денешься, в основном гранит науки по зубам лишь усидчивым. Да и вдохновение, как говорил великий Чайковский, — это птичка, которая посещает трудолюбивых. (Не ручаемся за точность цитаты, но смысл такой). Так что — вперед от простыхлогико–графических схем — к сложным!

СХЕМЫ ПРОСТЫЕ И СЛОЖНЫЕ

Из всего предшествующего материала мы уже поняли, что логико–графическая структура может быть и проше и сложнее (см. рис. 142а и 1426).

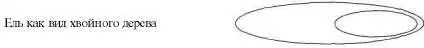
Рис. 142а

Рис. 1426

Эти две схемы явно проще, чем четырехугольники (рис. 100), автомобили (рис. 50), состав общества (рис. 75), мягкая конфронтация (рис. 120), причинно–следственные цепи в таянии льда после того, как ветер разогнал тучи и выглянуло солнце (рис. 127). Еще более сложна схема–таблица Менделеева.

Но природа сложности тоже может бытъразной.

Договоримся сначала, что простой схемой мы будем называть логико–графическое соединение двух понятий, как на последних двух рисунках. «Схема» — понятие стихийное. «Простая» — тоже понятие стихийное. Мы не будем давать им определений — и так все ясно. А вот понятию «простая схема» мы только что дали конвенциональное определение. О «конвенциональных» и «стихийных» понятиях мы подробно рассуждали выше, на с. 91–93.

Примеры простых схем — для закрепления (см. рис. 143).

В рамках одного и того же вида соотношения понятий может быть соединено не только два, но три и более понятий. Мы убеждались в этом уже неоднократно, но ради системности изложения теперь мы записали это отдельной строкой.

Объединение трех и более понятий — частый случай в классификационном соотношении понятий, видами которого являются родовидовое, рядоположное и перекрестное. Вряд ли нам имеет смысл приводить схемы–примеры читателю, проработавшему материат книги до сего места. Скорее всего, он сам может это сделать уже в порядке тренинга и обратиться для сверки к схемам на с. 63–91.

То же с частями и целым. Пусть читатель сам приведет примеры и сверит их со схемами на с. 96–99.

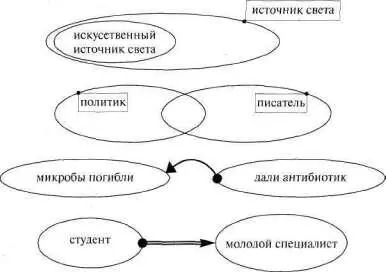
Рис. 143

То же и с причинно–следственными схемами. Свои примеры можно сверить со схемами на с. 102—104.

А вот пример объединения нескольких понятий в рамках трансформации (см. рис. 144).

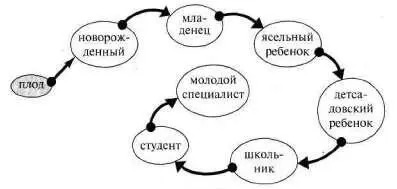
Рис. 144

Аналогичного примера до сих пор не было.

Объединение трех и более понятий в рамках одного и того же вида соотношения понятий назовем сложной ОДНОПЛАНОВОЙлогико–графической схемой. И закрепим за словосочетанием «сложная одно–плановая схема» объединение трех и более понятий именно и только в рамках одного и того же вида соотношения понятий. Как в выше приведенных примерах. Сложные одноплановые схемы могут быть на самом деле очень емкими, то есть включать много понятий, которые входят в многочисленные хитросплетения друг с другом. Примером может служить классификационная схема четырехугольников (см. рис. 100).

Если же три понятия и более объединены в рамках разных видов понятийных соотношений, то такие схемы мы будем называть сложными РАЗНОПЛАНОВЫМИ. Это еще одно конвенциональное понятие, введенное нами и используемое далее именно в таком смысле. Теперь об этом более подробно. Итак,