Капра Фритьоф - Паутина жизни. Новое научное понимание живых систем

Пример такой последовательности взят из их статьи и воспроизведен, в виде семи стадий, на рис. 9–1. В начальном состоянии (стадия 1) одна позиция решетки занята катализатором, а все другие — субстратами. На стадии 2 уже создано несколько звеньев, и, соответственно, теперь в решетке есть несколько дырок. На стадии 3 создано еще больше звеньев и некоторые из них образовали цепи. На стадиях 4–6 производство звеньев и формирование цепей продолжается, и на стадии 7 мы видим, что цепь связанных звеньев замкнулась на себя, охватив катализатор, три звена и два субстрата. Таким образом, цепь сформировала оболочку, проницаемую для субстрата, но не для катализатора. Как только случается такая ситуация, замкнутая цепь может стабилизироваться и превратиться в границу автопоэзной сети. Так случилось и в этой конкретной последовательности. Последующие стадии имитации на компьютере показали, что время от времени некоторые звенья границы могут случайно распадаться, но рано или поздно они заменяются новыми звеньями, созданными внутри оболочки в присутствии катализатора.

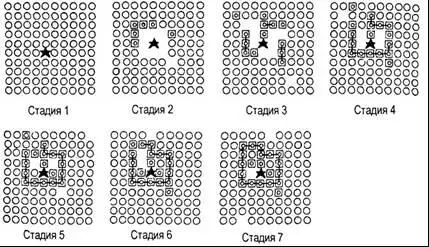
Рис. 9–1. Компьютерная имитация автопоэзной сети

В ходе длительной имитации цепь и дальше служила оболочкой для катализатора, тогда как звенья продолжали распадаться и заменяться другими. Таким образом, мембраноподобная цепь превратилась в границу сети преобразований, принимая при этом участие в деятельности этой же сети. Другими словами, была смоделирована автопоэзная сеть.

Будет ли последовательность такой имитации генерировать автопоэзный паттерн или не будет, в значительной мере зависит от вероятности распада, т. е. от того, насколько часто распадаются звенья. Поскольку тонкое равновесие между распадом и «починкой» основано на случайном движении субстратов сквозь мембрану, случайном создании новых звеньев и случайном перемещении этих звеньев к месту починки, мембрана будет оставаться стабильной только в том случае, если все эти процессы с большой вероятностью завершаются раньше, чем происходит следующий распад. Авторы показали, что при очень маленькой вероятности распада жизнеспособные автопоэзные паттерны действительно могут быть получены13.

Двоичные сети

Клеточный автомат, разработанный Варелой и его коллегами, стал одним из первых примеров того, как можно моделировать самоорганизующиеся сети живых систем. За последние двадцать лет было изучено множество других имитаций; показано, что эти математические модели способны спонтанно генерировать сложные высокоупорядоченные паттерны, в которых проявляются некоторые важные принципы порядка, наблюдаемые в живых системах.

Эти исследования получили новый толчок, когда стало ясно, что недавно разработанные элементы теории динамических систем — аттракторы, фазовые портреты, схемы бифуркации и т. п. — могут быть использованы в качестве эффективных инструментов для анализа моделей математических сетей. Взяв на вооружение эти новые методы, ученые снова обратились к двоичным сетям, разработанным в 40-е годы, и обнаружили, что, хотя это не автопоэзные сети, их анализ приводит к удивительным открытиям в области сетевых паттернов живых систем. Значительную часть этой работы выполнил биолог-эволюционист Стюарт Кауффман совместно с коллегами в институте Санта-Фе, Нью-Мехико14.

Поскольку изучение сложных систем с помощью аттракторов и фазовых портретов во многом связано с развитием теории хаоса, перед Кауффманом и его коллегами встал естественный вопрос: какова роль хаоса в живых системах? Мы и теперь еще далеки от полного ответа на этот вопрос, однако работа Кауффмана привела к нескольким интереснейшим идеям. Чтобы понять их, нам придется более пристально рассмотреть двоичные сети.

Двоичная сеть состоит из узлов, или переключателей, каждый из которых может находиться в одном из двух состояний, обычно обозначаемых ВКЛ и ВЫКЛ. То есть эта сеть более ограничена в возможностях, чем клеточный автомат, клетки которого могут находиться больше чем в двух состояниях. С другой стороны, узлы двоичной сети не обязательно образуют регулярную решетку, но могут быть соединены между собой более сложными способами.

Двоичные сети называют также «булевыми сетями», по имени английского математика Джорджа Буля, который использовал двоичные («да-нет») операции в середине XIX века для разработки символической логики, известной теперь как булева алгебра. На рис. 9–2 показана простая двоичная, или булева, сеть с шестью переключателями, каждый из которых подключен к трем соседним, причем два переключателя находятся в состоянии ВКЛ (черный цвет), а четыре — ВЫКЛ (белый цвет).

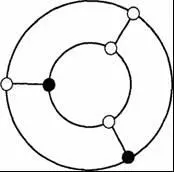
Рис. 9–2. Простая двоичная сеть

Как и в случае клеточного автомата, паттерн переключателей ВКЛ-ВЫКЛ в двоичной сети меняется дискретным образом. Переключатели соединены между собой так, что состояние каждого переключателя определяется предыдущими состояниями соседних переключателей в соответствии с некоторыми «правилами переключения». Например, для сети, изображенной на рис. 9–2, мы можем выбрать следующее правило: переключатель перейдет в состояние ВКЛ на следующем шаге, если по меньшей мере двое из его соседей на этом шаге будут находиться в состоянии ВКЛ; во всех других случаях А остается в состоянии ВЫКЛ.

На рис. 9–3 показаны три последовательности, образовавшиеся по этому правилу. Мы видим, что последовательность А достигает стабильного паттерна, в котором все переключатели находятся в состоянии ВКЛ, через два шага; последовательность В после первого шага колеблется между двумя дополняющими друг друга паттернами; паттерн же С стабилен с самого начала, воспроизводя себя в каждом шаге. Чтобы проанализировать подобные последовательности математически, каждый паттерн, или состояние, сети определяют шестью двоичными (ВКЛ-ВЫКЛ) переменными, т. е. всего двенадцатью переменными. В результате каждого шага система переходит из определенного состояния в определенное последующее состояние, в полном соответствии с правилом переключения.

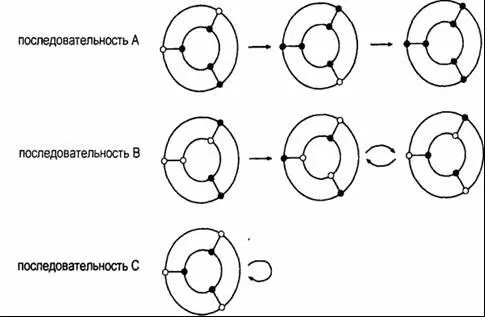
Рис. 9–3. Три последовательности состояний в двоичной сети

Как и в системах, описываемых дифференциальными уравнениями, каждое состояние изображается точкой в 12-мерном фазовом пространстве15. По мере того как, шаг за шагом, сеть переходит из одного состояния в другое, последовательность состояний вычерчивает траекторию в этом фазовом пространстве. Для классификации траекторий различных последовательностей применяется концепция аттракторов. Так, в нашем примере, последовательность А, которая движется к стабильному состоянию, связана с точечным аттрактором, тогда как колеблющееся состояние В соответствует периодическому аттрактору.