Ден Томел - Поиск неисправностей в электронике

5. Приведите таблицу истинности для схемы исключающее ИЛИ.

6. Сравните характеристики рассеяния мощности для схем ТТЛ и КМОП.

7. Назовите три способа определения связи входов и выходов при программировании программируемых логических приборов.

8. Назовите производителя, семейство, подсемейство, тип детали и тип корпуса для прибора с маркировкой DM74S00N.

9. Назовите три возможных причины обрыва на входе логической ИМС.

10. Опишите разницу между признаками обрыва и короткого замыкания.

11. Назовите четыре меры предосторожности, которые предотвращают перегрев компонентов.

12. Дайте определение явлению тиристорного защелкивания в схемах КМОП.

13. Назовите три меры предосторожности, которые вы можете предпринять для предотвращения повреждения ИМС МОП от электростатического разряда.

14. Назовите три способа избежать тиристорного защелкивания в схемах КМОП.

15. Назовите основное преимущество цифрового осциллографа по сравнению с аналоговым.

16. Назовите основное преимущество аналогового осциллографа по сравнению с цифровым.

17. Назовите три меры предосторожности, которые необходимо выполнить при ремонте оборудования.

18. Опишите процесс извлечения ИМС из платы.

19. Опишите процесс очистки паяльника для обеспечения максимальной передачи тепла и качественных паяных соединений.

20. Назовите три причины, по которым применение панельки для интегральной схемы может быть неуместно.

21. Дайте определения отверстиям с гальваническим покрытием в печатных платах.

В главе 7 был дан обзор основных типов логических элементов. Каждый из этих приборов имеет одно стабильное логическое состояние на выходе в ответ на определенную комбинацию входных сигналов. Многие из этих схем можно соединить вместе для построения более сложных комбинационных структур. Но определенное сочетание входных сигналов в известный момент времени всегда дает предсказуемый выходной сигнал 1 или 0.

Логические схемы с памятью, судя по названию, отвечают на входные сигналы различным способом, в зависимости от их предыдущего состояния. Другими словами, они реагируют на последовательность входных сигналов. Это придает другое измерение анализу таких схем, где учитывается время и предыдущее состояние.

В этой главе описаны некоторые типичные логические схемы с памятью, а также методы их тестирования и оценки их действия. Описываются различные элементы, которые используются для построения схем с памятью, а также их применение для построения более сложных схем. Поскольку в данной главе рассматриваются различные приборы и системы, здесь указаны некоторые простейшие способы контроля работоспособности с применением минимума оборудования, а также более сложные методы тестирования. Представленный учебный пример демонстрирует применение схем комбинированной логики и схем с памятью.

Всем нам хорошо знакомая десятичная система счисления основана на цифрах от 0 до 9. Комбинируя эти значения, мы можем представить бесконечное количество с целью подсчета или различения объектов друг от друга. В цифровых системах также необходимо работать с числами. К сожалению, в двоичной системе только два символа: 0 и 1. Сочетая эти базовые значения, мы также можем представить бесконечное число.

Мы считаем в десятичной системе: от 0 до 9. Для представления следующей величины нам необходимо использовать вторую цифру, расположенную на одну позицию влево, которая представляет собой число, кратное 10, показывающее, сколько раз мы посчитали до десяти (от 0 до 9). Каждый раз, когда мы досчитали от 0 до 9, следующий разряд увеличивается на единицу (инкрементируется), а в младшем разряде опять появляется 0, свидетельствующий о переходе на новый десяток.

Двоичная система счисления работает точно так же. Символы 0 и 1 называются двоичными цифрами, или, для краткости, битами. После того, как последняя значащая цифра становится равной 1, она сбрасывается в 0, а следующий разряд слева инкрементируется, что представляет количество двоек в числе. Следующий разряд слева представляет количество четверок, следующий — восьмерок и т. д. С каждым разрядом число увеличивается вдвое (таб. 8.1).

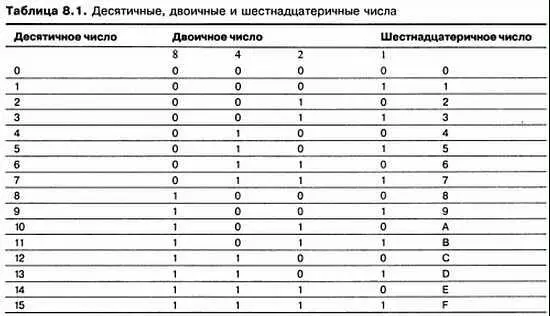
Сталкиваясь с большими двоичными числами, трудно отслеживать нули и единицы. Один из способов решения этой проблемы заключается в преобразовании двоичных чисел в десятичные с помощью сложения удельного веса разрядов, в которых находятся 1. Например:

8 4 2 1

1 1 0 1 - двоичное = 8 + 4 + 1 = 13 — десятичное

При больших двоичных числах такое преобразование становится сложным и порождает много ошибок. Более простой и распространенный способ представления больших двоичных чисел заключается в их преобразовании в шестнадцатеричную систему счисления.

Шестнадцатеричная система счисления использует 16 символов, поэтому она является системой с основанием 16. Первые 10 символов такие же, как в десятичной системе — от 0 до 9. Остальные 6 символов — это буквы от А до F, представляющие десятичные числа 10–15 соответственно.

Причина привлекательности шестнадцатеричной системы заключается в том, что преобразование чисел между ней и двоичной системами счисления выполняется очень просто. Для преобразования двоичного числа в шестнадцатеричное двоичное число делится на группы по 4 бита, начиная с наименее значимого бита (правого). Каждая группа из 4 битов затем непосредственно преобразуется в эквивалентный шестнадцатеричный символ, как указано в табл. 8.1. Приведенный ниже пример иллюстрирует типичное преобразование.

1010011101 — > 10 1001 1101 —> 29D

Шестнадцатеричная система счисления не меняет того факта, что цифровые системы работают с двоичными числами. Она просто упрощает нам обращение со значениями в двоичной системе. Гораздо проще использовать число 29D, чем 1010011101, при этом оба они представляют ту же величину. Более подробно с системами счисления и преобразованиями между ними вы можете познакомиться в любом из многих популярных изданий.

Базовые элементы, которые были рассмотрены в главе 7 , используются для построения более сложных комбинационных логических приборов, имеющих самую разную структуру, каждая их которых обладает собственными свойствами. Рассмотрим некоторые наиболее популярные и распространенные типы ИМС комбинационной логики.

Дешифраторы

Комбинационные приборы чаще всего выступают в качестве дешифраторов и шифраторов. Декодирование можно рассматривать как выявление соответствующего некоему условию входного двоичного сигнала с соответствующей реакцией на выходе. На рис. 8.1 показан элемент И-НЕ с четырьмя входами, который используется для декодирования величины 0В шестнадцатеричное (1011 двоичное).