В Бессонов - Радиоэлектроника для начинающих (и не только)

Формулу (2.1) можно записать иначе:

U= I∙ R. (2.2)

Из этой формулы видно: чем меньше сопротивление R проводника при одной и той же силе тока I , протекающей через проводник, гем меньше напряжение U , требуемое для протекания этого тока через этот проводник.

Зная силу тока I , протекающего через проводник, а также напряжение U , приложенное к концам проводника, из формулы (2.1) можно определить сопротивление R этого проводника:

R= U/ I. (2.3)

При пользовании этими формулами обратите особое внимание иа соответствие размерностей входящих величин. Сила тока I должна быть выражена в амперах, напряжение U в вольтах, а сопротивление R в омах. Для того чтобы запомнить закон Ома, можно из картона вырезать равносторонний треугольник и оформить его, как показано на рис. 2.14. Искомую величину (силу тока I , напряжение U или сопротивление R ) закрывают пальцем на треугольнике, а взаимное расположение двух оставшихся открытыми величин укажет, какие арифметические действия над ними необходимо произвести: на левом нижнем рисунке — умножение, на правых рисунках — деление.

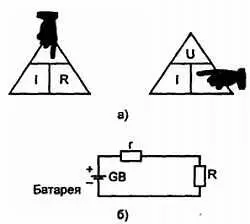
Рис. 2.14. Который позволяет быстро записать формулы для закона Ома

Решим несколько примеров.

• Вычислить силу тока I, протекающего через проводник, имеющий сопротивление R = 5 Ом, если к нему приложено напряжение U = 1,5 В.

Решение . I= U/ R= 1,5/5 = 0,3 А.

• К электрической лампе накаливания приложено напряжение U = 220 В, при этом через нее протекает сила тока I = 300 мА. Вычислить сопротивление нити накала.

Решение. Так как сила тока выражена в миллиамперах, преобразуем в амперы. Учитывая, что 1 А = 1000 мА, составим пропорцию:

1 А — 1000 мА,

I А — 300 мА.

Отсюда I= 1∙300/1000 = 0,3 А.

А теперь вычислим сопротивление нити накала:

R= U/ I= 220/0,3 = 733 Ом.

• Человек случайно коснулся руками двух проводов, находящихся под напряжением U = 220 В. Сопротивление человеческого тела R = 36 кОм (оно различно для различных людей). Чему равна сила тока, проходящего через тело человека? ( Это опасно для жизни, поэтому проводов, находящихся под напряжением, касаться нельзя! )

Решение .Преобразуем килоомы в омы. Так как 1 кОм = 1000 Ом, то 36 кОм = 36000 Ом. Тогда:

I= U/ R= 220/36000 = 0,006 А = 6 мА.

Каждый источник питания обладает внутренним сопротивлением. И на нем так же, как и на других элементах цепи, создается какое-то напряжение. С учетом этого напряжение на зажимах источника питания будет всегда меньше э.д.с. (электродвижущей силы) как раз на величину падения напряжения на внутреннем сопротивлении. Если увеличится потребляемая от источника питания сила тока, то в полном согласии с законом Ома увеличится и падение напряжения на внутреннем сопротивлении источника, а значит, уменьшится напряжение на зажимах источника питания.

Чтобы изменение нагрузки (изменение силы тока) меньше влияло на выходное напряжение источника, его внутреннее сопротивление стараются свести к минимуму.

Напряжение батарейки уменьшается и при ее старении, так как со временем увеличивается ее внутреннее сопротивление.

Закон Ома для полной цепи (с учетом внутреннего сопротивления источника) запишется так (рис. 2.14, б ):

I= Е/( R+ r). (2.1, б )

Здесь Е — э.д.с. источника питания; R — сопротивление нагрузки; r — внутреннее сопротивление источника питания.

В практике вам часто придется иметь дело с проводами при изготовлении трансформаторов, катушек индуктивности и в других случаях. Сопротивление провода вычисляется по формуле:

R= ρ∙ I/ S(2.4)

Здесь R — сопротивление провода в омах (Ом), I — его длина в метрах (м), S — площадь поперечного сечения в квадратных миллиметрах (мм 2).

S= 1,57∙ d 2

где d — диаметр провода в миллиметрах (мм); ρ — коэффициент пропорциональности, зависящий от рода материала, называется удельным сопротивлением материала, измеряется в омах, умноженных на метр (Ом∙м). Его значения для различных материалов приведены в таблице ПЗ. Приложения.

• Решим еще пример . Какой площади сечения S1 нужно взять алюминиевую проволоку, чтобы ее сопротивление R1 было такое же, как у железной проволоки (R2) сечением S 2= 2 мм 2? Длина обеих проволок одинакова ( l 1= l 2).

Запишем исходные условия по другому.

Дано: R1= ρ 1∙ l 1/ S 1; R2= ρ 2∙ l 2/ S 2. По условию задачи: R1 = R2 = R; l 1= l 2= l; S 1= 2 мм 2.

Из таблицы ПЗ Приложения:

ρ 1 = 2,5∙10 -8Ом∙м; ρ 2 = 12∙10 -8Ом∙м.

Определить S 1.

Тогда ρ 1∙ l 1/ S 1= ρ 2∙ l 2/ S 2. Отсюда:

S 1 = S 1= r 1∙ S 2/ ρ 2= 2,5∙10 -8= 0,41 мм 2. Ответ: S 1= 0,41 мм 2.

Вернитесь еще раз к формуле (2.4) и запомните размерность величин, которые должны подставляться в формулу.

На рис. 2.15 приведена номограмма для расчета сопротивления проводов с высоким удельным сопротивлением. Приведен пример (пунктирная линия) определения сопротивления манганинового провода диаметром 0,22 мм. Оно равно 3 Ом на каждый метр.

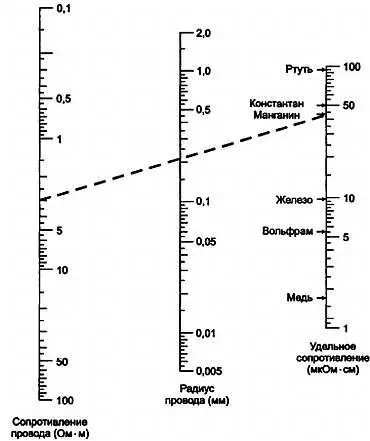
Рис. 2.15. Номограмма для расчёта сопротивления проводов с большим удельным сопротивлением

Известно, что при повышении температуры сопротивление металлов увеличивается. У некоторых металлов это увеличение значительно: у чистых металлов оно достигает 40…50 %. Такие сплавы, как константан и манганин имеют очень малое изменение сопротивления от температуры. Зависимость сопротивления металлов от температуры используется для устройства термометров сопротивления. Его (термометр из металла) помещают внутрь, например, печи, а концы обмотки включают в электрическую цепь.

Измеряя сопротивление обмотки, можно определить температуру в печи (рис. 2.16, а ). Такие термометры часто применяются для измерения очень высоких и очень низких температур, при которых ртутные термометры уже неприменимы.

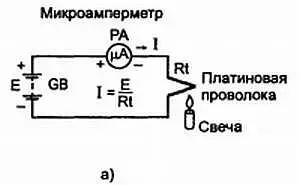
Рис. 2.16. а ) Термометр сопротивления, который позволяет измерять высокие и низкие температуры