Александр Кульский - КВ-приемник мирового уровня? Это очень просто!

«А»:Остынь, дружище! И, чтобы не тратить время напрасно, послушай, что в действительности представляет из себя вышепредложенная схема! Ты уже знаешь, что с возрастанием частоты индуктивное сопротивление ( X L) увеличивается, а емкостное сопротивление ( Х С) — уменьшается! Но отсюда следует, что при некоторой частоте f 0— индуктивное и емкостное сопротивления становятся равными. И в этот момент общее реактивное сопротивление цепи СТРЕМИТСЯ К НУЛЮ! Вспомним о сдвигах по фазе!

Так вот, когда частота генератора равна никакого сдвига по фазе между напряжением и током — НЕ БУДЕТ! Эта ситуация получила название — РЕЗОНАНС!

«Н»:Я знал, что есть механический резонанс…

«А»:Ну, примеры потрясающих случаев механического резонанса можно найти даже в Библии. Например, Иерихонские трубы!

«Н»:Действительно…

«А»:Итак, мы видим, что электрическая цепь, состоящая из емкости С и индуктивности L , обладает собственной резонансной частотой f 0! При этом общее сопротивление цепи становится очень малым, а амплитуда колебаний тока в ней — очень большой!

«Н»:Но почему ты говоришь «очень малым», а не говоришь — «нулевым»?

«А»:Ты прав, мой милый граф! Это только из-за того, что индуктивность L — это ведь изолированный провод, намотанный на сердечник. А провод, как известно, имеет еще и активное сопротивление, хотя и очень небольшое. Поэтому, в реальном случае, предыдущая схема выглядит так (рис. 3.8).

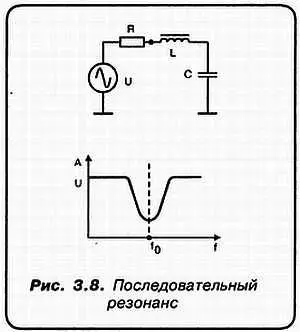
«Н»:А я готов нарисовать АЧХ этой схемы! Смотри, я даже учел тот факт, что из-за наличия активного сопротивления R «провал» АЧХ не имеет общей точки с осью абсцисс!

«А»:Я начинаю думать, что если дело и дальше пойдет так же успешно, то не только я, но и Спец запишется на цикл твоих лекций по электронике! Ну, а теперь я прошу тебя подумать, что будет в таком случае (рис. 3.9)…

Да, учти следующее обстоятельство. То, о чем мы сейчас говорим, я имею в виду электрический резонанс, — это «святая святых» радиотехники вообще и техники радиоприема, в частности!

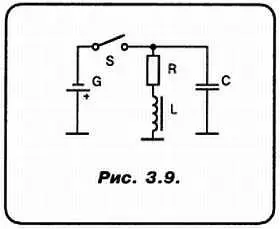
«Н»:Что я вижу!? Ты заменил генератор переменного тока на батарейку? К чему бы это?

«А»:Мы подключили батарейку к нашей схеме посредством выключателя, а затем отключили ее! Вот с этого момента мы и начнем анализ…

«Н»:А что же тут анализировать? Конденсатор просто разрядится через резистор R и индуктивность L ! И все дела!..

«А»:Да, кроме шуток?

«Н»:Нет-нет, прости! Не совсем… Что-то еще здесь произойдет… Но я пока не врубился — что!..

«А»:Вспомни, Незнайкин, что индуктивность L обладает некоторой инерцией. Образно говоря, из-за нее электронам так же трудно начать упорядоченное движение, как и прекратить это движение!

Ток разряда, проходя по виткам индуктивности L , порождает магнитное поле, в котором запасается некоторая энергия! Таким образом, в тот момент, когда конденсатор С уже разрядится, магнитное поле будет поддерживать упорядоченное движение электронов в том же направлении! Это значит, что до того момента, как энергия магнитного поля иссякнет, конденсатор успеет перезарядиться почти до первоначального напряжения! Хотя и ПРОТИВОПОЛОЖНОЙ ПОЛЯРНОСТИ! Затем снова наступит цикл перезаряда. И так будет продолжаться до того момента, пока на активном сопротивлении R (а оно в неявном виде ВСЕГДА присутствует в рассматриваемой системе) постепенно не перейдет в тепло ВСЯ первоначально запасенная в конденсаторе энергия!

«Н»:А рассмотренная система, состоящая из L, С и R , не имеет имени собственного?

«А»:Обязательно! И отныне мы будем употреблять только его — КОЛЕБАТЕЛЬНЫЙ КОНТУР!

«Н»:А как долго будет продолжаться подобная циркуляция тока в контуре? От чего это зависит?

«А»:Есть такой удивительный параметр — ДОБРОТНОСТЬ! Вот он то и, определяет, как долго в контуре будут продолжаться колебания.

«Н»:А почему ты назвал этот параметр — «удивительным»?

«А»:Да хотя бы потому, что он как бы един в трех лицах!

«Н»:А это как?

«А»:Да вот, посмотри на рисунок! На рис. 3.10, а изображены незатухающие электромагнитные колебания, которые имели бы место в контуре без потерь. На рис. 3.10, б изображены реальные, ЗАТУХАЮЩИЕ колебания в контуре.

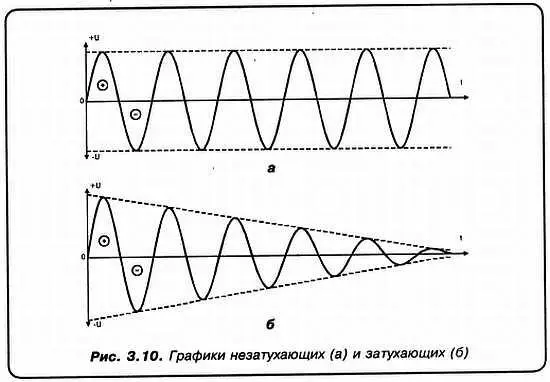
Так вот, численно, количество полных циклов заряд — разряд до, практически, полного затухания РАВНО ДОБРОТНОСТИ! Т. е. добротность Q = n , где n — количество полных циклов. А теперь от амплитудно-временных характеристик перейдем к АЧХ (рис. 3.11).

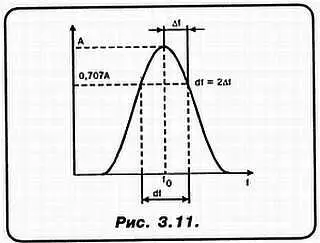
Вот эта, колоколообразная кривая (мы к ее рассмотрению вернемся в дальнейшем еще не раз) дает вторую, практически очень важную характеристику для Q :

Q= f 0/2 Δf,

где Δf — полоса пропускания по уровню 0,707.

И, кроме того, вот третья ипостась добротности, численно равная:

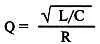
И если первая ипостась очень понятна, но не очень наглядна, поскольку кто успеет подсчитать точное число колебаний за очень малый промежуток времени, то вторая ипостась — может прямо выводиться на экран специальных анализаторов АЧХ! С ней удобно работать!

«Н»:Ну, а третья?

«А»:Третья ипостась — для реальных расчетов! Но любой колебательный контур характеризуется еще и частотой резонанса, или, что адекватно, частотой собственных колебаний:

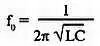
Любопытно, что для получения одной и той же f 0, можно взять различное соотношение L и С . Но формула для определения добротности показывает, каким именно должно быть соотношение L и С для получения требующейся нам ПОЛОСЫ ПРОПУСКАНИЯ КОЛЕБАТЕЛЬНОГО КОНТУРА! Она обозначена как df= 2 Δf

«Н»:А какого порядка эта величина должна быть?

«А»:Смотря для чего! А вообще получение высоких добротностей — это сложная техническая задача! Но, в общем, вполне решаемая! Сейчас нам осталось рассмотреть еще одну важную физическую, а равно и техническую особенность колебательных контуров!