Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

Однако в 1299 г. власти города Флоренция ввели указ, запрещающий их употреблять, объясняя это тем, что арабские цифры легко подделать: из 0 просто сделать 6 или 9. (Как будто этого нельзя сделать и с римскими цифрами.) Изворотливые купцы нашли выход из положения: бухгалтерские книги велись с использованием римских цифр, а черновые расчеты — арабских цифр. Поистине изобретательность деловых людей не знает границ.

Еще не раз власти пытались наложить запрет на арабские цифры. Так было, например, и в 1494 г., когда бургомистр города Франкфурт призывал конторщиков отказаться от их применения. Однако победа арабским цифрам была уже обеспечена: появляются многочисленные учебники и руководства по новой арифметике; торговые города заводят своих учителей, которые обучают работников торговых предприятии индо-арабской арифметике.

В русских городах в начале XVIII в. появились так называемые "цифирные" школы, где обучали арабскому счету. В 1703 г. талантливый педагог первой в России математико-навигационной школы Л.Ф. Магницкий издал свой знаменитый учебник "Арифметика", где использовались арабские цифры.

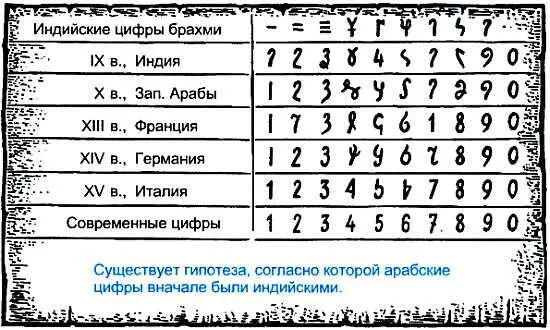
Арабские цифры не сразу приняли современный вид. Их эволюция начинается с индийских цифр брахми. Цифры 1, 2 и 3 получались из горизонтальных черточек брахми вследствие скорописной их записи. Вообще, форма цифр стабилизировалась только в XV в. в связи с появлением книгопечатания.

К концу XVIII в. арабская система нумерации победила повсеместно. И сейчас значение десяти цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9— понимают все народы в мире.

Почему вот уже на протяжении нескольких веков на всем земном шаре пользуются десятью арабскими цифрами, хотя не во все времена и не везде люди имели дело с арабской арифметикой? Прежде чем ответить на этот вопрос, познакомимся с одним замечательным свойством нашей системы счисления — позиционностью.

Изобразим какое-нибудь число, например 777. В нем один и тот же знак "7" участвует 3 раза, но когда он стоит справа, то означает семь единиц, когда в центре — семь десятков, когда слева — семь сотен. Таким образом, при записи числа цифра может иметь начертание одно и то же, а числовые значения — разные, в зависимости от места, позиции, на которой она стоит.

Такой принцип представления чисел называется поместным, или позиционным. Для записи любых сколь угодно больших чисел достаточно десяти цифр!

Каждая позиция, или разряд, числа имеет определенный "вес" (единицы, десятки, сотни и т. д.), поэтому число 777 можно расписать как

777 = 7∙10 2+ 7∙10 + 7,

т. е. как семь сотен плюс семь десятков и плюс семь единиц, а число, скажем, 4608 — следующим образом:

4608 = 4∙10 3+ 6∙10 2+ 0∙10 + 8,

т. е. как четыре тысячи плюс шесть сотен плюс нуль десятков и плюс восемь единиц.

Если призвать на помощь алгебру и вместо чисел записать буквы, то можно получить такую общую форму представления числа:

М= а n∙10 n+ а n-1∙10 n-1 + а 1∙10 + a 0

или сокращенную — через коэффициенты, если опускать степени числа 10:

М= ( а nа n-1… а 1a 0)

"Мы все учились понемногу", поэтому должны, конечно же, знать, что число 10 является основанием системы счисления. Коэффициенты а 0(число единиц), a 1(число единиц второго разряда, т. е. десятков), а 2(число единиц третьего разряда, т. е. сотен) и т. д. могут принимать значения, не превышающие основания системы: от 0 до 9. Эти коэффициенты можно получить формальным нулем как остатки от последовательного деления числа М на основание системы, т. е. на 10:

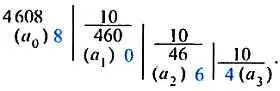
Цифры, полученные в остатке и последнем результате деления (они выделены синим цветом), и дают искомое изображение числа в десятичной позиционной системе счисления. Такая формальная процедура, лишенная, вообще говоря, смысла для десятичной системы, незаменима, как мы увидим, для систем с другими основаниями.

Примером непозиционнойсистемы счисления является римская нумерация. Так, в числе II единица в левой позиции имеет "вес", равный 1, а такая же единица в числе IX — "вес", равный минус 1. В числе XXXV (35) цифра X во всех позициях означает одно и то же — 10 единиц.

Основное преимущество позиционных систем счисления — удобство записи чисел и выполнения арифметических операций. Об этом мы узнаём с первого класса школы: сложение и умножение — "столбиком", деление — "углом" (для сравнения попробуйте перемножить римские числа…). По-видимому, в этом и заключена одна из основных причин того, что наша система счисления, будучи позиционной, завоевала столь прочные позиции.

Однако наблюдательный читатель может возразить: ведь две из древних систем счисления — двадцатеричная индейцев-майя и шестидесятеричная древних вавилонян — являются практически совершенными позиционными системами.

Вы правы, читатель. У вавилонян и индейцев-майя существовал позиционный принцип записи чисел. Напомним, что в арифметике майя одно и то же число, записанное в первом и во втором разрядах, отличалось одно от другого в 20 раз (т. е. в число раз, равное основанию системы); у вавилонян же прямой "клин" мог означать и 1, и числа, кратные 60, а одинаковые числа, помещенные в разные разряды, отличались в 60, 60 2,60 3и т. п. число раз.

Более того, в 1665 г. французский математик Б. Паскаль показал, что за основание системы счисления можно принять любое число, а это значит, что каждое число можно представлять в виде комбинации степеней не числа 10, а какого-либо другого целого числа. Выберем, например, число 7:

М= а n∙7 n+ а n-1∙7 n-1 + а 1∙7 + a 0

Ясно, что значения коэффициентов а 0 а 1…., a nдолжны теперь быть не больше нового основания, т. е. 7: они могут принимать значения от 0 до 6.

Представим число 777 в семеричной системе, используя принцип последовательного деления его на основание этой системы:

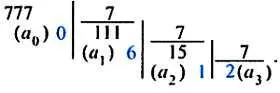
В результате число 777 10— так оно записано в десятичной системе — можно разложить по степеням основания 7:

(777) 10= 2∙7 3+ 1∙7 2+ 6∙7 + 0.