Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

Если опустить степени числа 7, как мы делаем при записи чисел в десятичной системе, то получим семеричную запись этого числа: ( 2 160) 7. Здесь цифра 7 в индексе указывает основание системы.

Действуя аналогичным образом, убедимся, что основание привычной для нас десятичной системы — теперь нам придется писать 10 10— будет изображаться в новой для нас семеричной системе как (13) 7. Число (147) 10будет в этой системе "круглым" и равным (300) 7. Точно так же (343) 10= (1 000) 7,т. е. и это число "круглое". Само основание семеричной системы (7) 10запишется символом (10) 7.

Возможно, если бы у человека на руках было не десять, а семь пальцев, то мы бы считали сейчас не десятками, а семерками, и более привычной нам казалась бы семеричная система счисления, в которой сложение выполняется знакомым нам "столбиком" (с переносом единицы в старший разряд, если сумма больше 6), а таблица умножения — даже проще, чем наша.

— Но ведь тогда, — воскликнет все тот же дотошный читатель, — естественно предположить, что до того, как человек пришел к десятичному счислению, он пользовался при счете пальцами одной руки, значит, могло возникнуть и распространиться пятиричное счисление. Догадка не лишена оснований.

В пятиричной позиционной системе всего пять цифр: 0, 1, 2, 3, 4. В ней число 777 будет представляться количеством "пятерок", "двадцатипяток" и т. д.:

(777) 10= 1∙5 4+ 1∙5 3 + 1∙5 2+ 0∙5 + 2= (11 102) 5.

Когда-то пятиричным счислением пользовались (т. е. считали "пятерками") многие народы. Следы этой системы сохранились в римской нумерации: в ней кроме знаков для единицы, десяти, ста, тысячи есть специальные знаки для пяти (V), пятидесяти (L) и пятисот (D).

Еще один след счета "пятерками" можно найти в записи чисел у индейцев племени ацтеков, населявших в XI–XVI вв. территорию Мексики. Единицу они обозначали точкой, двойку — двумя точками и т. д. до пяти. В запись числа 6 входила вертикальная черта, отделявшая пять первых точек от шестой. Ясно, что здесь счет велся группами по пять предметов. Черта отделяла одну такую группу от другой, причем сама черта никакого числа не обозначала.

Вот как описывает счет "пятерками" у жителей Новой Гвинеи известный русский путешественник Н.Н. Миклухо-Маклай:

"Папуас загибает один за другим пальцы руки, причем издает определенный звук, например бе, бе, бе …. Досчитав до пяти, он говорит ибон-бе (рука). Затем он загибает пальцы другой руки, снова повторяет бе, бе… , пока не доходит до ибон-али (две руки). Затем он идет дальше, приговаривая бе, бе… , пока не доходит до самба-бе и самба-али (одна нога, две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого".

Если же теперь наш настойчивый читатель сумеет пересчитать большим пальцем левой руки суставы оставшихся четырех пальцев, то, несомненно, заподозрит существование когда-то на заре человечества и двенадцатеричной системы счисления. Он и тут не ошибется! Так, короадосы Бразилии считают по числу суставов на каждом пальце левой руки (без большого) до 12, затем каждый палец правой руки (включая большой) означает 12. Двенадцатеричная система встречается у некоторых племен Центральной Америки.

Еще не так давно был распространен счет по дюжинам (т. е. число 12), дюжинам дюжин — "гроссам", дюжинам гроссов — "массам" для белья, посуды, писчебумажных товаров. Дома у нас сервизы содержат по 12 чашек, 12 блюдец, 12 тарелок.

О широком распространении двенадцатеричной системы свидетельствуют такие факты: мы до сих пор делим год на 12 месяцев; у англичан в системе мер 1 фут равен 12 дюймам, а в денежной системе 1 шиллинг равен 12 пенсам. Число 12 часто встречается также в сказках и легендах (12-главый змей, 12 братьев-разбойников), что говорит о древнем происхождении этой системы счисления.

Посмотрим, как будет представлено в ней число 777. Поскольку в системе должно быть двенадцать цифр, а мы знаем только десять, то придется ввести еще две цифры, обозначив 10, скажем, буквой А, а 11 — буквой Б. Осуществив последовательное деление нашего числа на основание 12, получим

(777) 10= 5∙12 2+ 4∙12 + 9= ( 549) 12

Число (35) 10=2∙12 + 11 запишется как (2Б) 12, а число (134) 10= 11∙12 + 2 - как (Б2) 12, т. е. оно станет двузначным.

Как видите, можно придумать много различных позиционных систем счисления, отличающихся только основаниями. И вес они, вообще говоря, равнозначны: ни одна из них не имеет явных преимуществ перед другой! Так почему же все-таки мы пользуемся именно десятичной системой счисления?

Вряд ли можно дать на этот вопрос исчерпывающий ответ. Одну из причин мы указали - 10 пальцев на руках человека. Возможно, системы с низким основанием (например, пятеричная) оказались менее пригодными, чем десятичная, потому что в них даже сравнительно небольшие числа выражались довольно громоздко. Или, может быть, использование системы с высоким основанием, таких как двадцатеричная или шестидесятеричная, не оправдалось на практике, поскольку требовалось запоминать большое число особых слов - названий низших числительных. Вероятно, поэтому в процессе естественного отбора в подавляющем большинстве случаев выжила система счисления с основанием "средней" величины, т. е. десятичная.

Число 2 - это самое меньшее из чисел, которое можно взять за основание системы счисления. Поэтому в двоичной системе счисления всего две цифры: 0 и 1. С их помощью можно "сосчитать" любые числа. Ведь мы уже убедились в том, что системы счисления с любым основанием равноправны.

Число в двоичной системе запишется так:

M = a n∙2 n+ a n-1∙2 n-1+ ... + a 1∙2 + a 0

Если в десятичной системе "вес" каждой позиции (или разряда) числа равен 10 в некоторой степени, то в двоичной системе вместо числа 10 используется число 2. "Веса" первых 13 позиций (разрядов) двоичного числа имеют следующие значения:

Попробуем записать уже привычное нам число (777) 10в двоичной системе счисления. Мы сможем легко сделать это, вспомнив принцип последовательного деления числа на основание системы, в данном случае числа 777 на число 2:

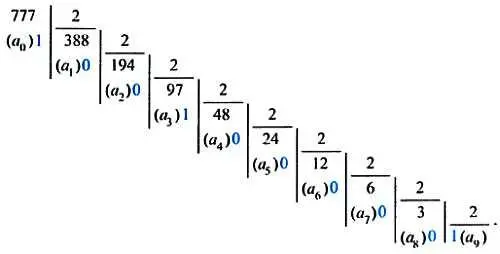
Представляя наше число в виде разложения по степеням двойки и отбрасывая потом при записи сами степени, получаем его запись в двоичной системе:

(777) 10= 1∙2 9 + 1∙2 8 + 0∙2 7 + 0∙2 6 + 0∙2 5 + 0∙2 4 + 1∙2 3 + 0∙2 2 + 0∙2 + 1 = ( 1100001001) 2