Евгений Айсберг - Цветное телевидение?.. Это почти просто!

Если же амплитуды не идентичны, то замирание будет частичным и передача, хотя и заглушённая, будет все же слышна (рис. 41).

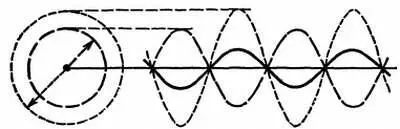
Рис. 41. Изображенные здесь колебания также находятся в противофазе, но они имеют разные амплитуды. Слагаемые синусоиды показаны пунктирными линиями, а результирующая — сплошной линией.

По счастливому совпадению обе волны могут оказаться в фазе. Тогда эти два колебания будут взаимно усиливаться. Ты можешь легко сложить две соответствующие синусоиды (рис. 42).

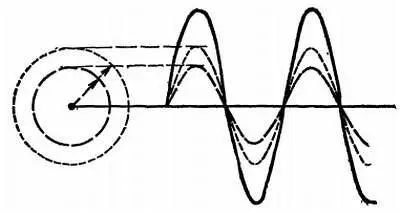
Рис. 42. Сложение двух колебаний с одинаковой фазой.

Но становится довольно трудно воспринимать передачу, когда две синусоиды смещены по фазе и в довершение всего имеют разные амплитуды. А ведь это наиболее распространенный случай. И тогда радиослушатель вынужден заниматься скучной работой по сложению (когда амплитуды имеют одинаковую направленность) или по вычитанию (когда они направлены в противоположные стороны) амплитуд для разных точек.

Рис. 43. Более сложный случай: сложение двух сдвинутых по фазе колебаний.

Хочешь ли ты, чтобы я открыл тебе секрет значительно более простого способа, который освободит тебя от трудоемких вычислений и позволит найти характеристики результирующего колебания, т. е. определить его фазу и амплитуду?

Ну ладно, этот секрет — векторное сложение . Название тебе ничего не говорит? Тогда прочитай описанное далее.

Прежде всего пойми, что вместо синусоиды можно начертить просто образующий ее вектор. Его длина дает нам информацию об амплитуде колебаний, а его направление — об их фазе.

Впрочем, ты можешь представить себе, что вектор вращается в темной комнате и что на каждом обороте короткая вспышка света позволяет нам его увидеть. Вспышки производятся с той же частотой, с которой вращается вектор, тогда при любой скорости движения он покажется нам неподвижным. Это принцип стробоскопа.

Заменив синусоиды векторами, ты, несомненно, заметишь тот факт, что векторы остаются неподвижными один относительно другого лишь до тех пор, пока частота колебаний остается идентичной.

Ты хочешь сложить две синусоиды? Просуммируй их векторы. Как это сделать? Очень просто, помести второй вектор так, чтобы его начало совпало с концом первого. Сумма этих векторов представлена третьим вектором, у которого исходная точка общая с первым, а конец совпадает с концом второго (рис. 44).

Рис. 44. Для сложения двух векторов их размещают так, чтобы конец одного совпал с началом другого.

Проверь сказанное мною на рассмотренном примере сложения двух синусоид. Два противоположно направленных вектора идентичной длины взаимно уничтожаются. Если длины этих векторов различны, то их сумма представляет собой разность их длин, а ее ориентация соответствует направлению более длинного вектора. Когда же сдвиг фазы отличается от 180°, векторное сложение позволяет определить амплитуду и фазу результирующего колебания.

Я добавлю, что вместо того, чтобы помещать начало одного вектора у конца другого, можно строить параллелограммы (рис. 45). (Ты, вероятно, изучал это в курсе механики).

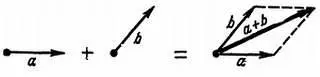
Рис. 45. Сложение векторов с помощью классического метода параллелограмма.

Оба вектора размещают так, чтобы их исходные точки совпали. Через конец каждого вектора проводят прямую, параллельную другому вектору, и таким образом получают параллелограмм; его диагональ, проведенная через общее начало векторов, точно соответствует сумме этих векторов.

Ты видишь, насколько изобретенное французским физиком Френелем векторное отображение синусоид упрощает изучение и анализ схем переменного тока. Зная, что индуктивность вызывает сдвиг фазы напряжения по отношению к току назад на 90° и что емкость, наоборот, сдвигает ток по отношению к напряжению вперед на 90°, легко вычертить диаграмму Френеля для схемы, состоящей из катушек индуктивности, конденсаторов и резисторов (последние, как известно, не сдвигают фазу тока по отношению к напряжению).

Дело существенно усложняется, когда складываются различные колебания, имеющие неодинаковую частоту. Примером в этом отношении могут служить ВЧ колебания, модулированные по амплитуде колебаниями низкой частоты. Известно, что в этом случае образуются две боковые частоты модуляции: низшая I и высшая S . Соответствующие векторы вращаются относительно вектора Р . Частота S выше частоты Р , и, следовательно, ее вектор вращается быстрее вектора Р .

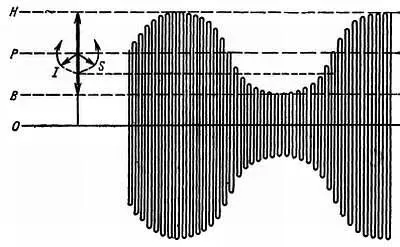
Рис. 46. При модулировании несущей Рпо амплитуде появляются две боковые полосы, изображенные двумя расположенными симметрично, но вращающимися в противоположных направлениях векторами Iи S. Сложение (всех трех векторов) дает один результирующий вектор, длина которого изменяется от ОВдо ОН.

Тогда при стробоскопическом освещении вектор Р кажется неподвижным, а вектор S вращающимся в направлении, обратном движению часовой стрелки. В то же время вектор более низкой частоты I вращается в противоположном направлении.

Сумма всех трех векторов всегда ориентирована в том же направлении, что и Р , так как I и S всегда расположены симметрично по отношению к Р . Следовательно, никакого изменения фазы не происходит. Зато амплитуда изменяется от максимума P + 2 S до минимума Р — 2 S .