Евгений Айсберг - Радио и телевидение?.. Это очень просто!

И, наконец, как и любой проводник, наш отрезок провода способен удерживать некоторый электрический заряд — как отрицательный, так и положительный. А это значит, что он обладает также и некоторой емкостью.

Все, что характерно для простого прямого отрезка провода, присуще, разумеется, и катушке: кроме своего основного свойства индуктивности, она обладает также некоторым активным сопротивлением и некоторой емкостью. Конденсатор, в свою очередь, помимо характеризующей его емкости имеет некоторое, обычно очень малое, активное сопротивление. В самом деле, проходя по обкладкам конденсатора, электрические заряды пересекают некоторую массу обкладок, обладающую небольшим активным сопротивлением. И эти небольшие перемещения зарядов порождают также индукцию.

Таким образом, вы видите, что ни одна из этих трех характеристик, обозначаемых буквами R, L и С , не может существовать отдельно без наличия двух других. Тем не менее мы не будем учитывать эти побочные явления, так как они неизмеримо меньше основного свойства компонента.

Нам необходимо изучить соединение однородных и разнородных компонентов. Мы проанализируем, какая величина получается в результате и какое сопротивление прохождению тока оказывают соединенные между собой компоненты.

Компоненты могут соединяться последовательно или параллельно (рис. 31).

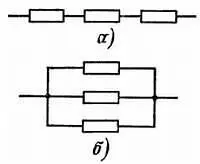
Рис. 31. Последовательное ( а) и параллельное ( б) соединения компонентов.

Последовательным соединением называется такое, когда конец одного компонента соединен с началом другого и т. д. В этом случае ток поочередно проходит по всем образующим цепочку компонентам. При параллельном соединении между собой соединены одноименные выводы. Здесь ток, разветвляясь, одновременно проходит по всем соединенным таким образом компонентам.

Вы легко поймете, что соединенные последовательно сопротивления складываются. Возьмем резисторы сопротивлением 100, 500 и 1000 Ом. Соединим их последовательно; полученная цепочка будет иметь сопротивление

R = 100 + 500 + 1000 = 1600 Ом.

Возьмем теперь катушки индуктивности и соединим их последовательно. При условии, что между ними нет взаимной индукции, их индуктивности должны складываться.

Возьмем катушки, обладающие индуктивностью соответственно 0,5 и 1,25 Г, и соединим их последовательно, разместив их достаточно далеко друг от друга, чтобы избежать взаимного влияния. Индуктивность цепи составит:

L = 0,5 + 1,25 = 1,75 Г.

Все это кажется очень простым. А будет ли так же просто при последовательном соединении конденсаторов?

Мы сказали, что при таком соединении сопротивления компонентов складываются. А у конденсаторов складываются емкостные сопротивления. Рассмотрим случай с двумя конденсаторами, имеющими емкости соответственно С 1 и С 2 , по которым протекает ток с частотой f (рис. 32).

Рис. 32. Последовательное соединение конденсаторов. Суммарная емкость меньше емкости каждого из них.

Емкостные сопротивления этих конденсаторов складываются и составляют общее емкостное сопротивление:

Рассматривая емкостное сопротивление всей цепочки как соответствующее емкости С , мы можем записать:

Умножив все члены этого равенства на 2 πf , получим

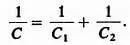
Проведенные преобразования позволяют нам сделать вывод, что при последовательном соединении конденсаторов нужно сложить обратные величины их емкостей, чтобы получить обратную величину емкости всей цепочки.

В рассмотренном нами случае, т. е. случае последовательного соединения двух конденсаторов, из последней формулы мы без большого математического усилия можем вывести формулу для расчета емкости всей цепочки:

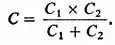
Перейдем теперь к изучению компонентов, соединенных параллельно. Этот способ включения облегчает прохождение тока. В самом деле, здесь складывают проводимости компонентов. Так называют величину, обратную сопротивлению.

Рассмотрим случай параллельного соединения активных сопротивлений (рис. 33).

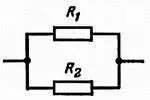
Рис. 33. При параллельном соединении резисторов общее сопротивление уменьшается.

Их проводимости 1/ R складываются. При параллельном соединении двух резисторов R 1 и R 2 проводимость всей цепочки 1/ R равна сумме проводимостей соединенных резисторов:

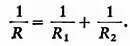
Как вы видите, здесь наблюдается аналогия с последовательным соединением конденсаторов, и вы без труда можете рассчитать общее сопротивление цепи R двух параллельно соединенных резисторов:

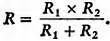
Теперь, если мои рассуждения вам еще не наскучили, рассмотрим случай параллельного соединения двух катушек, между которыми нет взаимной индукции (рис. 34).

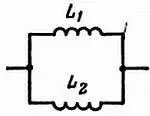
Рис. 34. Параллельное соединение катушек индуктивности.

Индуктивные сопротивления катушек пропорциональны их индуктивности. Следовательно, они будут вести себя аналогично активным сопротивлениям.

Итак, мы не ошибемся, если скажем, что две соединенные параллельно катушки L 1 и L 2 обладают общей индуктивностью, которая рассчитывается по формуле

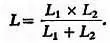
И, наконец, рассмотрим случай двух соединенных параллельно конденсаторов (рис. 35).

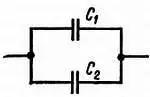
Рис. 35. Параллельное соединение конденсаторов.

Здесь нужно складывать проводимости, которые представляют собой величины, обратные емкостным сопротивлениям. Но сами емкостные сопротивления, как вы помните, обратно пропорциональны емкостям. Это означает, что проводимости конденсаторов прямо пропорциональны их емкостям.