Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Н. — Разумеется, до величины А , потому что конденсатор С был разряжен. Но тогда… по резистору R должен пройти ток, а это невозможно, так как конденсатор не может пропустить ток!

Л. — Не увлекайся. Да, сразу же после скачка входного напряжения по резистору R пойдет ток, и в начале его величина будет A / R . Ведь конденсатор имеет полное право пропустить ток, если этот ток заряжает, произойдет следующее: по мере заряда конденсатора С ток в резисторе R будет снижаться.

Н. — И, если подождать достаточно долго, С зарядится до напряжения А , после чего в R не будет тока, и U вых вновь станет равно нулю.

Л. — О, Незнайкин, как быстро ты все понимаешь сегодня! Выходное напряжение изменяется так, как я показал на рис. 66.

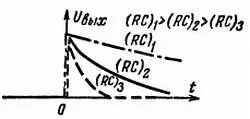
Рис. 66. Форма напряжения на выходе дифференцирующей схемы, на вход которой подается скачкообразно изменяющееся напряжение, изображенное на рис. 65. Пунктирной линией обозначена форма напряжения при малом произведении (RC) 3, сплошной — при среднем (RС) 2и штрих-пунктирной — при большом (RC) 1.

Скорость снижения напряжения определяется произведением R на С , которое называется постоянной времени схемы и выражается в секундах (при С в фарадах и R в омах). В самом деле, чем больше емкость конденсатора С при данном сопротивлении R , тем медленнее он заряжается; чем больше сопротивление резистора R (при данной емкости С ), тем больше времени требуется на заряд конденсатора. Можно легко доказать, что по истечении времени, равного постоянной времени RC, выходное напряжение падает примерно до 37 % величины А . По истечении удвоенного такого отрезка времени RC выходное напряжение составляет только 13,5 % величины А , после утроенного времени RC можно сказать, что выходного напряжения уже совсем нет, так как напряжение упало до 5 % величины А . Если произведение RC невелико, выходное напряжение изменяется, как показано пунктирной линией на рис. 66; при большой величине RC кривая принимает форму, показанную на рис. 66 штрих-пунктирной линией. При очень малой величине произведения RC кривая выходного напряжения имеет вид короткого сигнала импульсного типа (рис. 67).

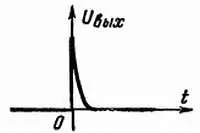
Рис. 67. Короткий импульс, получаемый на выходе дифференцирующей схемы с малым произведением (RC) 3при подаче на ее вход скачкообразно изменяющегося напряжения.

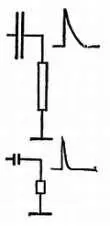
Н. — Хорошо, это я понял. Но напряжение, получаемое на выходе триггера Шмитта или амплитудного ограничителя, имеет совсем не такую форму, как на рис. 65. Оно состоит из чередующихся фронтов и срезов. Скажи, пожалуйста, что получится, если это напряжение (рис. 68, а ) подать на вход схемы, изображенной на рис. 64.

Л. — Фронт и срез — практически одно и то же, различие между ними лишь в направлении изменений. На выходе схемы срез даст нам отрицательный импульс (рис. 68, б ).

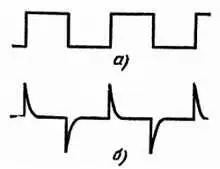
Рис. 68. Прямоугольный сигнал ( а) представляет собой периодическую последовательность резких подъемов и спадов. Дифференцирующая схема с малой постоянной RC превращает этот сигнал в чередующиеся положительные и отрицательные импульсы ( б).

Н. — В сущности это очень просто. Теперь я понимаю, почему ты так стремишься получить крутые фронт и срез: при медленном изменении напряжения конденсатор С успел бы зарядиться и перестал передавать изменения входного напряжения. Но и в этих условиях можно получить хороший результат, достаточно увеличить R или С (или обе величины) и тогда конденсатор С будет мало разряжаться во время изменения сигнала.

Л. — Незнайкин, ты сегодня определенно в прекрасной форме, но будь осторожен; если ты увеличишь произведение RC, может случиться, что между двумя сигналами конденсатор С не успеет полностью зарядиться; тогда выходное напряжение примет такую форму, которую я изобразил для тебя на рис. 69. Поэтому нужно сделать постоянную времени RC большой по сравнению с длительностью сигнала и малой по сравнению с периодом сигнала. Чем меньшую часть периода занимает сигнал, тем легче подобрать постоянную времени RC.

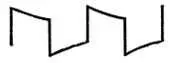
Рис. 69. Если постоянная времени RC-схемы достаточно велика по сравнению с периодом сигнала, то выходное напряжение принимает иную форму. Конденсатору Сне хватает времени полностью зарядиться.

Н. — Бедный сигнал, его совсем лишили человеческого лица! Исходную синусоиду (можно предположить, что сначала наш сигнал имел именно такую форму) с помощью триггера Шмитта превратили в прямоугольные сигналы, а затем в короткие импульсы с помощью твоей схемы с рис. 64… кстати, как называется эта схема?

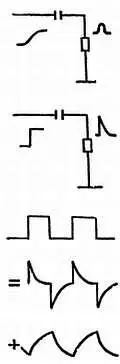
Л. — Ее называют дифференцирующей схемой . Как видишь, ты напрасно испугался этого названия. Но мы на этом не остановимся, ибо сигнал можно подвергнуть и другим деформациям. Что ты думаешь о схеме на рис. 70? Ее название я скажу тебе потом.

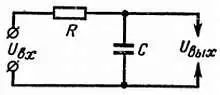
Рис. 70. Фильтр нижних частот, используемый в качестве интегрирующей схемы.

Н. — Это та же самая схема, что показана на рис. 64, только ты поменял местами R и С .

Л. — Но эта деталь все изменяет! Что мы получим на выходе схемы, если на ее вход подадим прямоугольные сигналы?

Н. — Здесь имеются резистор и соединенный с ним последовательно конденсатор, поэтому мы возможно получим то, что ты раньше нарисовал на рис. 68, б .

Л. — Какой ужас! Ведь я тебе объяснил, что «напряжение на выводах конденсатора не может измениться на конечную величину за равное нулю время». Но посмотри, Незнайкин, если на вход схемы (см. рис. 64) подать прямоугольные сигналы (см. рис. 68, а ) и если на выходе, т. е. на выводах резистора R, получим сигнал, изображенный на рис. 68, б то на выводах конденсатора должен быть такой сигнал, который, будучи прибавленным к сигналу на рис. 68, б , даст сигнал, показанный на рис. 68, а .