Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Н. — Ты хочешь сказать разность этих двух сигналов? Хорошо, я могу найти ее графически. Подожди минутку… интересующий тебя сигнал я начерчу на рис. 71.

Рис. 71. При подаче на вход интегрирующей схемы прямоугольного сигнала с большим по сравнению с постоянной времени RC периодом на выходе получают сигнал с округленными фронтами, очень мало похожий на входной сигнал.

Л. — Очень хорошо. Как ты видишь, на выводах конденсатора находится тот самый сигнал, который мы получим на выходе схемы, приведенной на рис. 70. Этого можно было ожидать. При изменении входного сигнала сигнал на выходе реагирует не сразу, так как требуется некоторое время, пока конденсатор С зарядится до нового напряжения.

Н. — Фронты и срезы твоего прямоугольного сигнала стали наклонными и округленными. Для чего нужен такой сигнал?

Л. — Такой сигнал, как ты нарисовал, действительно не представляет большого интереса. Но предположим, что я увеличу произведение RC. Как при этом изменится форма сигнала на выходе?

Н. — Я предполагаю, что конденсатор С получит меньше тока (он увеличился и его потребности возросли), и поэтому он не успеет зарядиться к моменту прихода второго сигнала. Вероятно, в результате получим сигнал, форма которого показана на рис. 72.

Рис. 72. При большей величине RC конденсатор Сне успевает полностью зарядиться между двумя изменениями напряжения.

Л. — Ты прав. Если еще увеличить RC, то выходное напряжение будет изменяться мало и выходной сигнал примет форму, изображенную на рис. 73.

Рис. 73. При дальнейшем увеличении произведения RC амплитуда выходного сигнала уменьшается.

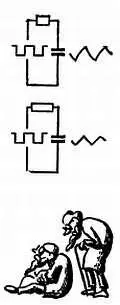
Н. — Смотри, твоя кривая состоит из прямых отрезков!

Л. — Так оно и есть. Выходное напряжение по сравнению с входным мало, и можно сказать, что напряжение на выводах резистора R в интервалах между переходами почти постоянное. Следовательно, зарядный (или разрядный) ток остается почти постоянным и конденсатор С заряжается (или разряжается) почти линейно. Чтобы ты мог лучше видеть форму напряжения на выходе, я увеличил масштаб полученной кривой по вертикали (рис. 74).

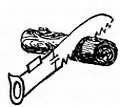
Рис. 74. Если выходной сигнал (рис. 73) вычертить в другом масштабе, четко видны почти равносторонние треугольники, напоминающие зубья пилы.

Н. — Странная форма, прямо как зубья пилы для пилки дерева.

Л. — Верно, по этой причине сигнал назвали «зубьями пилы» или «симметричным пилообразным сигналом». Его используют в тех случаях, когда нужно периодически и линейно изменять напряжение вверх и вниз. Это один из возможных случаев применения изображенной на рис. 70 схемы, которую называют интегрирующей.

Н. — Так вот почему ты не хотел сказать мне название схемы! Но скажи, пожалуйста, почему этим схемам дали такие жуткие названия.

Л. — Ну так, Незнайкин, ты сам захотел! Чтобы ответить на твой вопрос, необходимо хотя бы в самой общей форме объяснить, что такое производная и интеграл. Впрочем, это не очень разрядит твой мозг.

Функцией называют величину у , зависящую от другой величины х , которую называют переменной: каждому значению (причина) соответствует определенная величина у (следствие). Посмотри, как «реагирует» величина у на изменения переменной относительно заданного значения а . Иначе говоря, сравним изменения следствия с изменениями породившей их причины (рассчитав для этого коэффициенты этих изменений). Ответом может служить отклонение функции относительно точки а . Мы рассмотрим возможно малые изменения х относительно величины а , чтобы точнее установить, как ведет себя функция в окрестности величины а .

Как ты видишь, мы легонько «пощекочем» переменную (причину) и посмотрим, как это скажется на функции (следствии). Если следствие этого «щекотания» будет велико, мы скажем, что производная большая.

Если переменной служит время, а функцией — пройденным путь, то производной является скорость. Например, если для каждого момента известно место нахождения автомобиля на дороге, то мы можем рассчитать его скорость. Если в момент, который я обозначу t 0 , автомобиль находится в некотором месте, а в момент t 0 + 2 сек (т. е. 2 сек спустя) он находится на 30 м дальше, то я могу рассчитать его скорость, разделив прирост пройденного пути (30 м) на прирост времени (2 сек)

30 м: 2 сек = 15 м/сек (или 54 км/ч).

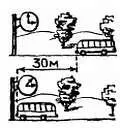
Следовательно, я могу сказать, что скорость в данном месте есть производная от пройденного пути по времени. Эта производная велика, когда пройденный путь быстро увеличивается с увеличением времени.

Н. — Довольно туманно. Мне представляется, что это несколько напоминает схему на рис. 64. Если входное напряжение увеличивается быстро, то зарядный ток конденсатора С будет большой, что даст большое напряжение на выходе.

Л. — Ты очень хорошо понял. Но в нашем примере с автомобилем, разумеется, не может быть резкого изменения пройденного пути, так как соответствующая этому изменению скорость была бы бесконечно большой…

Н. — Вот чему могли бы позавидовать все бегуны!

Л. — Но это невозможно, так как «бесконечно большую» скорость нужно было бы достичь за ничтожно малый отрезок времени, что в свою очередь требует бесконечно большого ускорения. Но поговорим теперь о математическом определении интегрирования. Ты можешь получить прекрасное представление на том же примере с автомобилем, если теперь предположить, что для каждого момента мы знаем не место машины на дороге, а ее скорость (например, зафиксировав самописцем показания спидометра). Задача сводится к определению пройденного автомобилем пути к соответствующему моменту времени.