Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

Частоты опорного и выходного сигналов с помощью цифровых средств делятся до частоты 400 кГц, на которой фазовый детектор работает лучше. Заметьте, что для преобразования синусоидального сигнала в сигнал с логическими уровнями используется вентиль типа `НС со смещением на логическом пороге с помощью резистора обратной связи большого номинала. Обратите внимание также на выходную ступень обычного эмиттерного повторителя (с ограничением по току), предназначенную для работы на 50-омный кабель, как показано на рис. 9.42. При настройке схемы ферритовый сердечник генератора подстраивается до получения полного размаха на выходе фильтра фазового детектора.

Фирма Motorola выпускает прекрасную серию недорогих ИМС «ФАПЧ-синтезатор частоты» МС145145-59, которые содержат фазовые детекторы типа 2 и делители по модулю n и для входного и для опорного сигналов; оба делителя программируются, точность 14 разрядов и более. Держите эти схемы на примете на тот случай, когда вам потребуется синтезировать какие-нибудь необычные частоты.

Псевдослучайные двоичные последовательности являют собой пример гармоничного сочетания аналоговой и цифровой техники. Оказывается, можно необычайно просто генерировать последовательности бит (или слов), с хорошими стохастическими свойствами, т. е. последовательности, которые будут обладать такими же вероятностными и корреляционными свойствами, какими обладает идеальная машина для подбрасывания монеты. Поскольку эти последовательности генерируются стандартными элементами детерминированной логики (если быть точнее, регистрами сдвига), получающиеся двоичные последовательности на самом деле являются предсказуемыми и повторяемыми, хотя любой фрагмент такой последовательности во всех отношениях выглядит как случайная последовательность 0 и 1. Всего с помощью нескольких ИМС можно получить последовательности, которые тянутся буквально на столетия без повторения; это очень простой и привлекательный способ получения цифровых двоичных последовательностей или аналоговых сигналов шума.

Действительно, существует даже недорогая ИМС «цифровой источник шума», выпускаемая в корпусе мини-DIP (ММ5437 фирмы National), а генераторы шума на регистрах сдвига входят в состав технических средств многих ИМС, создающих звуковые эффекты.

Аналоговый шум.С помощью простой фильтрации нижних частот псевдослучайной двоичной последовательности (ПСП) можно получить гауссов белый шум с ограниченной полосой, т. е. напряжение шума с плоским энергетическим спектром до некоторой частоты среза (более подробно о шумах см. гл. 7 ). С другой стороны, с помощью взвешенного суммирования содержимого регистров сдвига (с использованием набора резисторов) можно осуществить цифровую фильтрацию . С помощью этого способа можно легко получить плоский спектр шума в пределах нескольких мегагерц. Позже вы увидите, что источники аналогового шума, синтезированные цифровым способом, имеют целый ряд преимуществ перед чисто аналоговыми способами, использующими шумящие диоды или резисторы.

Другие области применения.Кроме таких очевидных применений, как аналоговые или цифровые источники шума, ПСП полезны в целом ряде других областей, ничего общего не имеющих с шумами. Их можно использовать для шифрования сообщений или данных, поскольку идентичный генератор ПСП на приемном конце дает ключ к шифру. ПСП широко используются в кодах, обнаруживающих и исправляющих ошибки, так как они позволяют видоизменить блоки данных таким образом, что правильные кодовые сообщения будут находится друг от друга на максимально возможном «расстоянии Хэмминга» (измеряется числом позиций с разными данными). Обладая хорошими автокорреляционными свойствами, они являются идеальными как коды для радиолокационных систем, в которых ответный сигнал сравнивается (точнее взаимно коррелируется) с передаваемой битовой последовательностью. Их можно использовать даже как компактные делители по модулю n .

Наиболее известным (и самым простым) генератором ПСП является регистр сдвига с обратной связью (рис. 9.82).

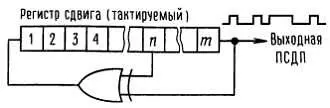
Рис. 9.82. Генератор псевдослучайной двоичной последовательности.

Регистр сдвига длины m работает от тактовых импульсов с частотой f 0 . Входная последовательность формируется с помощью вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ, на вход которого поступают сигналы от n -го и последнего ( m -го) разрядов регистра сдвига. Такая схема проходит через некоторое множество состояний (совокупность состояний регистра сдвига после каждого тактового импульса), которые после К тактов начинают повторяться, т. е. последовательность состояний является циклической с периодом К .

Максимальное число возможных состояний m -разрядного регистра равно К = 2 m , т. е. числу m -битовых двоичных комбинаций. Однако состояние «все нули» является «тупиком» для этой схемы, поскольку на выходе вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ появляется 0, который вновь поступает на вход схемы. Таким образом, последовательность максимальной длины, которую может сформировать данная схема, содержит 2 m — 1 бит. Оказывается, что такую последовательность максимальной длины можно получить только при правильном выборе m и n , причем полученная последовательность будет псевдослучайной. (Критерием максимальной длины является неприводимость и примитивность многочлена 1 + х n + х m над полем Галуа). В качестве примера рассмотрим 4-разрядный регистр сдвига с обратной связью, показанный на рис. 9.83.

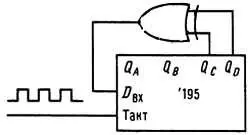
Рис. 9.83.

Начиная с состояния 1111 (можно было бы начать с любого другого состояния, за исключением 0000), можно записать состояния в порядке их следования:

Мы записали эти состояния как 4-разрядные числа Q A Q B Q C Q D. Здесь 15 = (2 4- 1) различных состоянии, затем они повторяются вновь. Значит, это регистр максимальной длины.

Упражнение 9.6. Покажите, что 4-разрядный регистр с обратной связью от второго и четвертого разрядов не является регистром максимальной длины. Сколько существует различных последовательностей? Сколько состояний в каждой последовательности?