Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

Для того чтобы осуществить взвешенное суммирование одновременно нескольких последовательных выходных разрядов, можно просто воспользоваться различными параллельными выходами разрядов регистра сдвига и использовать резисторы различного номинала, подключенные к суммирующей точке операционного усилителя. Для НЧ-фильтра весовые коэффициенты должны быть пропорциональны (sin x )/ x ; обратите внимание, поскольку весовые коэффициенты могут быть обоих знаков, потребуется инвертирование некоторых уровней. Так как в этой схеме не используются конденсаторы, выходной сигнал будет состоять из набора дискретных уровней выходного напряжения.

Используя весовую функция для большого числа разрядов последовательности, можно улучшить приближение к гауссову шуму. Более того, в этом случае аналоговый выходной сигнал становится фактически непрерывным сигналом. По этим причинам желательно использовать как можно больше выходов регистра сдвига, используя в случае необходимости дополнительные ступени регистра сдвига, включенные в обратную связь с вентилем ИСКЛЮЧАЮЩЕЕ ИЛИ. Как и ранее, для задания стабильных цифровых уровней напряжения следует использовать резисторную «подвеску» к питанию или КМОП-ключи (для этих целей КМОП-логика является идеальным решением, поскольку выходы при этом точно соответствуют U CC и земле).

Схема, показанная на рис. 9.90, генерирует псевдослучайный аналоговый шум, полосу которого можно менять с использованием рассмотренного способа в огромном диапазоне.

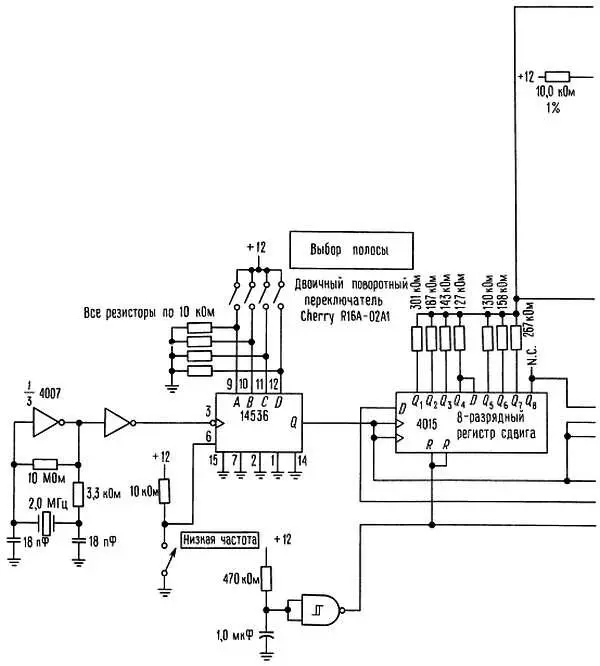
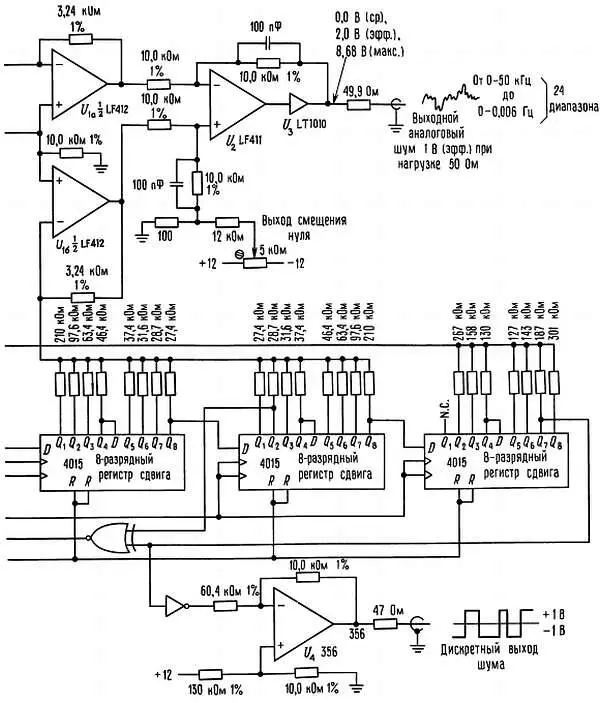
Рис. 9.90. Лабораторный генератор шума с широким частотным диапазоном.

Сигнал кварцевого генератора с частотой 2,0 МГц поступает на 24-разрядный программируемый делитель 14536, который формирует тактовую частоту от 1,0 МГц до 0,12 Гц с коэффициентом деления кратным 2. 32-разрядный регистр сдвига охвачен обратной связью от 31- и 18-го разрядов и генерирует последовательность максимальной длины с миллиардом состояний (на максимальной тактовой частоте полный цикл регистра проходит за полчаса). Здесь мы использовали взвешенное суммирование с функцией (sin x )/ x на 32 последовательных разрядах последовательности. Элементы Y 1 и Y 2 усиливают инвертированные и неинвертированные выходы соответственно и запускают дифференциальный усилитель Y 3 . Коэффициенты усиления выбираются таким образом, чтобы сформировать на 50-омной нагрузке напряжение 1,0 В ср. кв. без постоянной составляющей (2,0 В ср. кв. на холостом ходу). Обратите внимание на то, что эта амплитуда шума не зависит от тактовой частоты, т. е. от общей полосы. Такой цифровой фильтр имеет частоту среза на 0,05 f такт и формирует спектр белого шума от полосы постоянный ток ÷ 50 кГц (максимальная тактовая частота) до полосы постоянный ток ÷ 0,006 Гц (минимальная тактовая частота) на 24 диапазонах. Схема вырабатывает выходной сигнал от +1,0 до -1,0 В. Относительно этой схемы можно сделать несколько важных замечаний.

Обратите внимание на то, что в этой схеме в обратной связи используется инвертирующий вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ, поэтому инициализацию регистра можно осуществить простым обнулением. Использование инверсии входных последовательных сигналов исключает состояние «все единицы» (а не «все нули» как при использовании обычного вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ), но все другие свойства остаются в силе.

Взвешенное суммирование конечного числа битов не может сформировать настоящий гауссов шум из-за ограничения по амплитуде пика. Можно показать, что выходная амплитуда пика (на 50 Ом) составляет ±4,34 В, что дает коэффициент формы 4,34. Эти цифры имеют важное значение, поскольку для того, чтобы исключить эффект ограничения, коэффициент усиления Y 1 необходимо с помощью Y 2 поддерживать достаточно низким. Внимательно приглядитесь к методам, используемым для формирования выходных сигналов с нулевой постоянной составляющей из уровней КМОП со средним значением +6,0 В (низкий уровень — 0 В, высокий — +12 В).

Описанный метод цифровой низкочастотной фильтрации последовательностей максимальной длины используется во многих коммерческих генераторах шума.

Несколько заключительных замечаний относительно последовательностей, генерируемых регистрами сдвига, как источников аналогового шума. На основании трех перечисленных ранее свойств регистров максимальной длины вы, возможно, склонны заключить, что выходная последовательность «чересчур случайна» в том смысле, что она имеет точное число серий заданной длины и т. п. Настоящая случайная машина для подбрасывания монеты не генерировала бы на единицу больше «орлов», чем «решек», а ее автокорреляционная функция не была бы абсолютно плоской для конечной последовательности. Посмотрите на это с другой стороны. Если бы вы использовали единицы и нули, вырабатываемые регистром сдвига, для управления случайным блужданием, двигаясь вперед на один шаг при получении единицы и назад на один шаг при получении нуля, то оказались бы на расстоянии ровно в один шаг от начальной точки после того, как регистр пройдет весь цикл. Этот результат уж никак нельзя назвать случайным!

Вместе с тем упомянутые свойства регистра сдвига верны только для всей последовательности из 2 n — 1 бит, взятой как одно целое . Если вы используете фрагмент полной битовой последовательности, то его свойства будут довольно точно аппроксимировать случайный автомат для подбрасывания монеты. Представьте себе аналогичный процесс — извлечение красных и синих шаров наугад из урны, в которую вначале помещены К шаров (половина красных, половина синих). Если вы вытаскиваете шары без возвращения , то сначала вы рассчитываете получить почти случайную статистику. По мере убывания шаров в урне статистика изменяется за счет того, что общее число красных и синих шаров должно оставаться тем же самым.

Представление о том, как это происходит, можно получить, вновь вернувшись к случайному блужданию. Если предположить, что единственным «неслучайным» свойством последовательности является точное равенство «1» и «0» (не обращая внимание на одну лишнюю «1»), то можно показать, что описанное случайное блуждание после r вытаскиваний из общей «популяции» К /2 единиц и К /2 нулей приведет к среднему расстоянию от начальной точки, равному

Х= [ r( К— r)/( К— 1)] 1/2.