Пауль Хоровиц - Искусство схемотехники. Том 1 [Изд.4-е]

Изготовители этих интегральных схем предлагают для пользователей подробные расчетные формулы и таблицы. Они дают рекомендации по выбору номиналов сопротивлений внешних резисторов для получения фильтров Баттерворта, Бесселя и Чебышева разных порядков; при этом можно получать фильтры с характеристиками верхних, нижних частот или полосовые и полосноподавляющие. Привлекательной особенностью этих гибридных схем является то, что в модуль встроены конденсаторы; так что остается добавить только внешние резисторы.

Полосовые фильтры.Несмотря на большое число схемных элементов, фильтр, построенный на основе метода переменных состояния, представляется наиболее удачной схемой для реализации (высокодобротных) полосовых фильтров. Он обладает низкой поэлементной чувствительностью, не предъявляет высоких требований к ширине полосы пропускания ОУ, а также прост в настройке. Например, в представленной на рис. 5.18 схеме, используемой в качестве полосового фильтра, с помощью двух резисторов R F устанавливается центральная частота полосы пропускания, в то время как резисторы R Q и R G совместно определяют добротность Q и коэффициент усиления в полосе пропускания

R F = 5,03·10 7/ f 0Ом,

R Q = 10 5/(3,48 Q+ G— 1) Ом,

R G = 3,16·10 4 Q/ GОм.

Следовательно, можно сделать настраиваемый по частоте фильтр с фиксированной добротностью Q при использовании в качестве резистора R F двухсекционного переменного резистора (потенциометра). С другой стороны, переменным можно сделать резистор R Q , при этом получается фильтр с фиксированной частотой и изменяемой добротностью Q (и, к сожалению, с переменным коэффициентом передачи).

Упражнение 5.4.Необходимо рассчитать номиналы резисторов показанной на рис. 5.18 схемы, используемой в качестве полосового фильтра с f0 = 1 кГц, Q = 50 и G = 10.

На рис. 5.19 изображена полезная модификация полосового фильтра на основе метода переменных состояния.

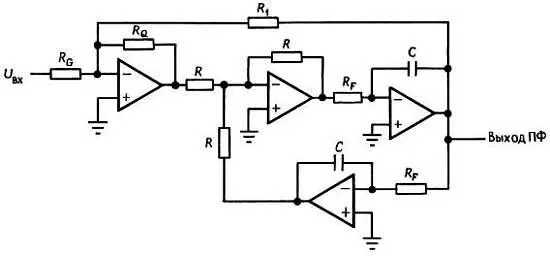
Рис. 5.19. Фильтр с независимой регулировкой усиления и добротности Q

Недостатком является использование в ней четырех ОУ, достоинство же заключается в возможности регулировать ширину полосы пропускания (т. е. добротность Q ) без изменения коэффициента усиления в полосе. Действительно, как добротность Q , так и коэффициент усиления устанавливаются единственным резистором. Добротность Q , коэффициент усиления и центральная частота полосы пропускания полностью независимы и задаются следующими простыми соотношениями:

f 0 = 1/2π R FC, Q= R 1/ R Q, G= R 1/ R G,

R ~= 10 кОм (значение некритично, подгоняемое).

Биквадратные фильтры. Наиболее близко к фильтру на основе метода переменных состояния примыкает изображенный на рис. 5.20 так называемый биквадратный фильтр. В этой схеме также используются три ОУ и ее можно сконструировать с помощью упомянутой ранее ИС на основе метода переменных состояния.

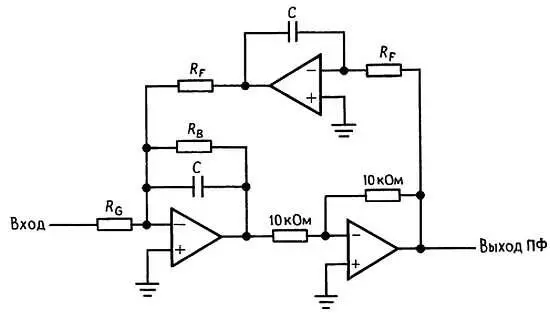
Рис. 5.20. Биквадратный фильтр.

Замечательным свойством такого фильтра является возможность регулировки его частоты (с помощью R F ) при сохранении постоянности ширины полосы пропускания (это предпочтительнее, чем сохранение неизменности добротности Q ). Далее предлагаются расчетные уравнения:

f 0 = 1/2π R FC, BW= 1/2π R BC, G= R B/ R G.

Сама добротность Q определяется как f 0 / BW и равна R B / R F . При изменении значения центральной частоты (с помощью R F ) пропорционально изменяется и добротность Q , при этом сохраняется неизменной ширина полосы пропускания Qf 0 .

Когда вы проектируете биквадратный фильтр вчерновую (правильнее использовать ИС активного фильтра, которая уже содержит большинство необходимых элементов), то основная методика определяется следующим образом:

1. Выберем ОУ с шириной полосы пропускания f с , которая по крайней мере в 10–20 раз превышает Qf 0 .

2. Подберем округленный номинал конденсатора, ближайший к следующему значению С = 10/ f 0 мкФ.

3. Используем требуемое значение центральной частоты для расчета значения сопротивления R F согласно приведенному выше первому уравнению.

4. Используем второе расчетное уравнение для вычисления по заданному значению ширины полосы пропускания номинала сопротивления R G .

5. Исходя из требуемого коэффициента передачи на центральной частоте полосы пропускания и согласно третьему расчетному уравнению получаем значение сопротивления R G .

Если расчетные значения сопротивлений получаются слишком велики или слишком малы, что неудобно в некоторых случаях, то можно подобрать другой номинал конденсатора. Например, в высокодобротном фильтре потребуется использовать увеличенное значение конденсатора С , отчасти с тем чтобы предотвратить существенное увеличение значение сопротивления R B (или можно использовать описанную в разд. 4.19 Т-образную цепь). Следует отметить, что каждое из сопротивлений R F, R B и R G является нагрузкой для ОУ и, следовательно, их значение не должно становиться меньше, скажем, 5 кОм. Манипулируя номиналами элементов схемы, можно найти их значения, так чтобы просто удовлетворялось требование 1 путем уменьшения коэффициента передачи интегратора (увеличение значения R F ) при соответствующем увеличении коэффициента передачи инвертирующего каскада (увеличение значения резистора обратной связи, которое в исходной схеме составляет 10 кОм).

Для иллюстрации предположим, что желательно спроектировать фильтр с теми же характеристиками, как в последнем упражнении. Мы должны начать с того, что временно зададим С = 0,01 мкФ. Затем найдем R F = 15,9 кОм ( f 0 = 1 кГц) и R B = 796 кОм ( Q = 50; BW = 20 Гц). Наконец, R G = 79,6 кОм ( G = 10).

Упражнение 5.5.Необходимо спроектировать полосовой фильтр со следующими параметрами: f0 = 60 Гц, BW = 1 Гц и G = 100.

Полосовые фильтры высокого порядка.Как и для рассмотренных ранее фильтров нижних и верхних частот имеется возможность проектировать полосовые фильтры более высоких порядков с приблизительно плоской полосой пропускания и крутым переходом к полосе задерживания. Это можно сделать с помощью каскадного соединения нескольких полосовых фильтров более низкого порядка, комбинируя их таким образом, чтобы обеспечить характеристику фильтра требуемого вида (Баттерворта, Чебышева и любые другие). Как и раньше фильтр Баттерворта имеет «максимально плоскую» характеристику, в то время как фильтр Чебышева удовлетворяет требованиям плоской характеристики в полосе пропускания при крутых скатах (переходной области).